
【题目】已知函数![]() (a为常数).
(a为常数).
(1)求不等式![]() 的解集;
的解集;
(2)当a>0时,若对于任意的![]() [3,4],
[3,4],![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【答案】(1)见解析(2)a>![]()
【解析】
(1)不等式化为![]() ,讨论①a=0、②a>0和③a<0时,求出对应不等式的解集;
,讨论①a=0、②a>0和③a<0时,求出对应不等式的解集;
(2)根据(1)得![]() 的解集,再根据[3,4]与解集包含关系列不等式解得结果.
的解集,再根据[3,4]与解集包含关系列不等式解得结果.
解:(1)不等式![]() 化为
化为![]() ,即
,即![]() ,
,
①a=0时,不等式变为![]() ,解得
,解得![]() <1;
<1;
②a>0时,不等式变为![]() ,
,
若a>2,则![]() <1,解得
<1,解得![]() >1或
>1或![]() <
<![]() ,
,
若a=2,则![]() =1,解得
=1,解得![]() ≠1,
≠1,
若0<a<2,则![]() >1,解得
>1,解得![]() >
>![]() 或
或![]() <1;
<1;
③a<0时,不等式变为(![]() -
-![]() )(
)(![]() -1)<0,解得
-1)<0,解得![]() <
<![]() <1;
<1;
综上所述,![]() =0时,不等式
=0时,不等式![]() 的解集为(-∞,1);
的解集为(-∞,1);
0<a<2时,不等式![]() 的解集(-∞,1)∪(
的解集(-∞,1)∪(![]() ,+∞);
,+∞);
a=2时,不等式![]() 的解集(-∞,1)∪(1,+∞);
的解集(-∞,1)∪(1,+∞);
a>2时,不等式![]() 的解集(-∞,
的解集(-∞,![]() )∪(1,+∞);
)∪(1,+∞);
a<0时,不等式![]() 的解集(
的解集(![]() ,1);
,1);
(2)由(1)知:①0<a<2时,![]() ,
,![]() (-∞,1)∪(
(-∞,1)∪(![]() ,+∞),
,+∞),
需[3,4](-∞,1)∪(![]() ,+∞),
,+∞),
∴![]() <3,即2<3a,解得2>a>
<3,即2<3a,解得2>a>![]() ;
;
②a=2时,![]() (-∞,1)∪(1,+∞),符合条件;
(-∞,1)∪(1,+∞),符合条件;
③a>2时,![]() (-∞,
(-∞,![]() )∪(1,+∞),符合条件;
)∪(1,+∞),符合条件;
综上所述,符合条件的a的取值范围是a>![]() .
.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
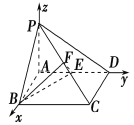
【题目】如图,在四棱锥PABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB=2,BC=2![]() ,E,F分别是AD,PC的中点.
,E,F分别是AD,PC的中点.
(1)证明:PC⊥平面BEF;
(2)求平面BEF与平面BAP夹角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校拟派一名跳高运动员参加一项校际比赛,对甲、乙两名跳高运动员进行了8次选拔比赛,他们的成绩(单位:m)如下:
甲:1.70,1.65,1.68,1.69,1.72,1.73,1.68,1.67;
乙:1.60,1.73,1.72,1.61,1.62,1.71,1.70,1.75.
经预测,跳高1.65m就很可能获得冠军.该校为了获取冠军,可能选哪位选手参赛?若预测跳高1.70m方可获得冠军呢?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是20个国家和地区的二氧化碳排放总量及人均二氧化碳排放量.
国家和地区 | 排放总量/千吨 | 人均排放量/吨 | 国家和地区 | 排放总量/千吨 | 人均排放量/吨 | |
A | 10330000 | 7.4 | K | 480000 | 2.0 | |
B | 5300000 | 16.6 | L | 480000 | 7.5 | |
C | 3740000 | 7.3 | M | 470000 | 3.9 | |
D | 2070000 | 1.7 | N | 410000 | 5.3 | |
E | 1800000 | 12.6 | O | 390000 | 16.9 | |
F | 1360000 | 10.7 | P | 390000 | 6.4 | |
G | 840000 | 10.2 | Q | 370000 | 5.7 | |
H | 630000 | 12.7 | R | 330000 | 6.2 | |
I | 550000 | 15.7 | S | 320000 | 6.2 | |
J | 510000 | 2.6 | T | 490000 | 16.6 |
(1)这20个国家和地区人均二氧化碳排放量的中位数是多少?
(2)针对这20个国家和地区,请你找出二氧化碳排放总量较少的前15%的国家和地区.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 的各棱长均相等,
的各棱长均相等, ![]() 底面
底面![]() ,E,F分别为棱
,E,F分别为棱![]() 的中点.
的中点.
(1)过![]() 作平面α,使得直线BE//平面α,若平面α与直线
作平面α,使得直线BE//平面α,若平面α与直线![]() 交于点H,指出点H所在的位置,并说明理由;
交于点H,指出点H所在的位置,并说明理由;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系中,直线![]() 的参数方程为
的参数方程为 (其中t为参数),现以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(其中t为参数),现以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)写出直线l普通方程和曲线C的直角坐标方程;
(2)过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 交
交![]() 于
于![]() ,
, ![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足f(x)=f(﹣4﹣x),f(0)=3,若![]() 是f(x)的两个零点,且
是f(x)的两个零点,且![]() .
.
(Ⅰ)求f(x)的解析式;
(Ⅱ)若x>0,求g(x)=![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某幼儿园雏鹰班的生活老师统计2018年上半年每个月的20日的昼夜温差![]() ,
,![]() 和患感冒的小朋友人数(
和患感冒的小朋友人数(![]() /人)的数据如下:
/人)的数据如下:
温差 |
|
|
|
|
|
|
患感冒人数 | 8 | 11 | 14 | 20 | 23 | 26 |
其中![]() ,
,![]() ,
,![]() .
.
(Ⅰ)请用相关系数加以说明是否可用线性回归模型拟合![]() 与
与![]() 的关系;
的关系;
(Ⅱ)建立![]() 关于
关于![]() 的回归方程(精确到
的回归方程(精确到![]() ),预测当昼夜温差升高
),预测当昼夜温差升高![]() 时患感冒的小朋友的人数会有什么变化?(人数精确到整数)
时患感冒的小朋友的人数会有什么变化?(人数精确到整数)
参考数据:![]() .参考公式:相关系数:
.参考公式:相关系数: ,回归直线方程是
,回归直线方程是![]() ,
, ,
,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com