
【题目】如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AB,E为线段PB的中点,F为线段BC上的动点.

(1)求证:AE⊥平面PBC;
(2)试确定点F的位置,使平面AEF与平面PCD所成的锐二面角为30°.
【答案】(1)见解析(2)当点F为BC中点时,平面AEF与平面PCD所成的锐二面角为30°
【解析】
(1)证明![]() .
.![]() ,推出
,推出![]() 平面
平面![]() .得到
.得到![]() .证明
.证明![]() ,得到
,得到![]() 平面
平面![]() .然后证明平面
.然后证明平面![]() 平面
平面![]() .
.
(2)分别以![]() 的方向为
的方向为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向,建立如图所示的空间直角坐标系
轴的正方向,建立如图所示的空间直角坐标系![]() ,设正方形
,设正方形![]() 的边长为2,求出为平面
的边长为2,求出为平面![]() 的法向量,平面
的法向量,平面![]() 的法向量,利用空间向量的数量积求解即可.
的法向量,利用空间向量的数量积求解即可.
解:(1)∵PA⊥平面ABCD,BC![]() 平面ABCD
平面ABCD
∴PA⊥BC
∵ABCD为正方形
∴AB⊥BC
又 PA∩AB=A,PA,AB![]() 平面PAB
平面PAB
∴BC⊥平面PAB
∴AE![]() 平面PAB
平面PAB
∴AE⊥BC
∵PA=AB,E为线段PB的中点
∴AE⊥PB
又 PB∩BC=B,PB,BC![]() 平面PBC
平面PBC
∴AE⊥平面PBC
(2)以A为坐标原点,建立如图所示的空间直角坐标系A-xyz,
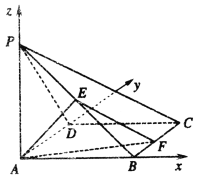
设正方形ABCD的边长为2,则A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0)P(0,0,2)E(1,0,1)
∴![]() ,
,![]() ,
,![]()
设F(2,λ,0)(0≤λ≤2),
∴![]()
设平面AEF的一个法向量为![]()
则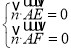
∴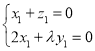
令y1=2,则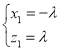
∴![]()
设平面PCD的一个法向量为![]()
则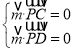
∴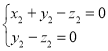
令y2=1,则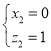
∴![]()
∵平面AEF与平面PCD所成的锐二面角为30°,
∴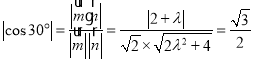 ,
,
解得λ=1,
∴当点F为BC中点时,平面AEF与平面PCD所成的锐二面角为30°


科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() .
.
(1)求曲线![]() 的直角坐标方程与直线l的参数方程;
的直角坐标方程与直线l的参数方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 处的切线斜率为2,试求a的值及此时的切线方程;
处的切线斜率为2,试求a的值及此时的切线方程;
(2)若函数![]() 在区间
在区间![]() (其中
(其中![]() …为自然对数的底数)上有唯一的零点,求实数a的取值范围.
…为自然对数的底数)上有唯一的零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的前n项和为Sn,a1=1,且4Sn,3Sn+1,2Sn+2成等差数列.
(1)求{an}的通项公式;
(2)若数列{bn}满足b1=0,bn+1﹣bn=1,设cn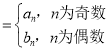 ,求数列{cn}的前2n项和.
,求数列{cn}的前2n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.某大学为了解在校本科生对参加某项社会实践活动的意向,拟采用分层抽样的方法从该校四个年级的本科生中抽取一个容量为300的样本进行调查.已知该校一、二、三、四年级本科生人数之比为6:5:5:4,则应从一年级中抽取90名学生
B.10件产品中有7件正品,3件次品,从中任取4件,则恰好取到1件次品的概率为![]()
C.已知变量x与y正相关,且由观测数据算得![]() =3,
=3,![]() =3.5,则由该观测数据算得的线性回归方程可能是
=3.5,则由该观测数据算得的线性回归方程可能是![]() =0.4x+2.3
=0.4x+2.3
D.从装有2个红球和2个黑球的口袋内任取2个球,至少有一个黑球与至少有一个红球是两个互斥而不对立的事件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】端午节是我国民间为纪念爱国诗人屈原的一个传统节日.某市为了解端午节期间粽子的销售情况,随机问卷调查了该市1000名消费者在去年端午节期间的粽子购买量(单位:克),所得数据如下表所示:
购买量 |
|
|
|
|
|
人数 | 100 | 300 | 400 | 150 | 50 |
将烦率视为概率
(1)试求消费者粽子购买量不低于300克的概率;
(2)若该市有100万名消费者,请估计该市今年在端午节期间应准备多少千克棕子才能满足市场需求(以各区间中点值作为该区间的购买量).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了更好地贯彻党的“五育并举”的教育方针,某市要对全市中小学生“体能达标”情况进行了解,决定通过随机抽样选择几个样本校对学生进行体能达标测试,并规定测试成绩低于60分为不合格,否则为合格,若样本校学生不合格人数不超过其总人数的5%,则该样本校体能达标为合格.已知某样本校共有1000名学生,现从中随机抽取40名学生参加体能达标测试,首先将这40名学生随机分为甲、乙两组,其中甲乙两组学生人数的比为3:2,测试后,两组各自的成绩统计如下:甲组的平均成绩为70,方差为16,乙组的平均成绩为80,方差为36.
(1)估计该样本校学生体能测试的平均成绩;
(2)求该样本校40名学生测试成绩的标准差s;
(3)假设该样本校体能达标测试成绩服从正态分布![]() ,用样本平均数
,用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差s作为
,用样本标准差s作为![]() 的估计值
的估计值![]() ,利用估计值估计该样本校学生体能达标测试是否合格?
,利用估计值估计该样本校学生体能达标测试是否合格?
(注:1.本题所有数据的最后结果都精确到整数;2若随机变量z服从正态分布,则![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,把满足条件
,把满足条件![]() (对任意的
(对任意的![]() )的所有数列
)的所有数列![]() 构成的集合记为
构成的集合记为![]() .
.
(1)若数列![]() 的通项为
的通项为![]() ,判断
,判断![]() 是否属于
是否属于![]() ,并说明理由;
,并说明理由;
(2)若数列![]() 的通项为
的通项为![]() ,判断
,判断![]() 是否属于
是否属于![]() ,并说明理由;
,并说明理由;
(3)若数列![]() 是等差数列,且
是等差数列,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com