
已知函数 .
.

(1)画出 a =" 0" 时函数 的图象;
的图象;
(2)求函数 的最小值.
的最小值.
(1)函数的图像的求解,对于二次函数的图像作对称变换可知道。
(2)当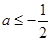 时,函数
时,函数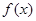 的最小值为
的最小值为
当 时,函数
时,函数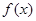 的最小值为
的最小值为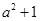
当a > 时,函数f (x)的最小值为
时,函数f (x)的最小值为 +a
+a
【解析】
试题分析:解:(1)略 4分
(2)①当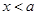 时,
时,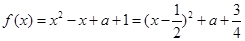 5分
5分
若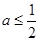 ,则函数
,则函数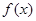 在
在 上单调递减,从而函数
上单调递减,从而函数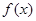 在
在 上的最小值为
上的最小值为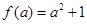
若 ,则函数
,则函数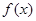 在
在 上的最小值为
上的最小值为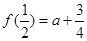 7分
7分
②当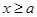 时,
时,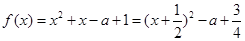 8分
8分
若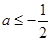 ,则函数
,则函数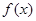 在
在 上的最小值为
上的最小值为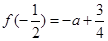
若 ,则函数
,则函数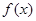 在
在 上的最小值为
上的最小值为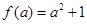 10分
10分
综上,当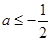 时,函数
时,函数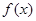 的最小值为
的最小值为
当 时,函数
时,函数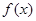 的最小值为
的最小值为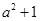
当a > 时,函数f (x)的最小值为
时,函数f (x)的最小值为 +a. 12分
+a. 12分
考点:函数的图像与值域
点评:解决的关键是对于绝对值函数的理解,要去掉绝对值符号,然后结合二次函数的性质来得到图像以及相应的值域,属于基础题。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| a |
| x |
| lnx |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| x |
| 3 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com