
【题目】如图,在平面直角坐标系xOy中,已知以M为圆心的圆M:x2+y2﹣12x﹣14y+60=0及其上一点A(2,4).
(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;
(2)设平行于OA的直线l与圆M相交于B、C两点,且BC=OA,求直线l的方程;
(3)设点T(t,0)满足:存在圆M上的两点P和Q,使得 ![]() ,求实数t的取值范围。
,求实数t的取值范围。
【答案】
(1)
解:∵N在直线x=6上,∴设N(6,n),
∵圆N与x轴相切,∴圆N为:(x﹣6)2+(y﹣n)2=n2,n>0,
又圆N与圆M外切,圆M:x2+y2﹣12x﹣14y+60=0,即圆M:((x﹣6)2+(x﹣7)2=25,
∴|7﹣n|=|n|+5,解得n=1,
∴圆N的标准方程为(x﹣6)2+(y﹣1)2=1.
(2)
解:由题意得 ![]() ,
, ![]() 设
设 ![]() ,则圆心
,则圆心 ![]() 到直线
到直线 ![]() 的距离
的距离 ![]() ,
,
则 ![]() ,
, ![]() ,即
,即 ![]() ,
,
解得 ![]() 或
或 ![]() ,即
,即 ![]() :
: ![]() 或
或 ![]()
(3)
解: ![]() ,即
,即 ![]() ,即
,即 ![]() ,
,![]() ,
,
又 ![]() ,即
,即 ![]() ,解得
,解得 ![]() ,
,
对于任意 ![]() ,欲使
,欲使 ![]()
![]() ,
,
此时 ![]() ,只需要作直线
,只需要作直线 ![]() 的平行线,使圆心到直线的距离为
的平行线,使圆心到直线的距离为 ![]() ,
,
必然与圆交于 ![]() 两点,此时
两点,此时 ![]() ,即
,即 ![]() ,
,
因此对于任意 ![]() ,均满足题意,
,均满足题意,
综上 ![]()
【解析】(1)设N(6,n),则圆N为:(x﹣6)2+(y﹣n)2=n2 , n>0,从而得到|7﹣n|=|n|+5,由此能求出圆N的标准方程.
(2)由题意得OA=2 ![]() ,kOA=2,设l:y=2x+b,则圆心M到直线l的距离:d=
,kOA=2,设l:y=2x+b,则圆心M到直线l的距离:d= ![]() ,由此能求出直线l的方程.
,由此能求出直线l的方程.
(3) ![]() =
= ![]() ,即|
,即| ![]() |=
|= ![]() ,又|
,又| ![]() |≤10,得t∈[2﹣2
|≤10,得t∈[2﹣2 ![]() ,2+2
,2+2 ![]() ],对于任意t∈[2﹣2
],对于任意t∈[2﹣2 ![]() ,2+2
,2+2 ![]() ],欲使
],欲使 ![]() ,只需要作直线TA的平行线,使圆心到直线的距离为
,只需要作直线TA的平行线,使圆心到直线的距离为 ![]() ,由此能求出实数t的取值范围.
,由此能求出实数t的取值范围.
【考点精析】认真审题,首先需要了解圆的一般方程(圆的一般方程的特点:(1)①x2和y2的系数相同,不等于0.②没有xy这样的二次项;(2)圆的一般方程中有三个特定的系数D、E、F,因之只要求出这三个系数,圆的方程就确定了;(3)、与圆的标准方程相比较,它是一种特殊的二元二次方程,代数特征明显,圆的标准方程则指出了圆心坐标与半径大小,几何特征较明显).


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos4x+sin2x,下列结论中错误的是( )
A. f(x)是偶函数
B. 函数f(x)最小值为![]()
C. ![]() 是函数f(x)的一个周期
是函数f(x)的一个周期
D. 函数f(x)在![]() 内是减函数
内是减函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有偶数个球,其中红球、黑球各占一半.甲、乙、丙是三个空盒.每次从袋中任意取出两个球,将其中一个球放入甲盒,如果这个球是红球,就将另一个球放入乙盒,否则就放入丙盒.重复上述过程,直到袋中所有球都被放入盒中,则( )
A.乙盒中黑球不多于丙盒中黑球
B.乙盒中红球与丙盒中黑球一样多
C.乙盒中红球不多于丙盒中红球
D.乙盒中黑球与丙盒中红球一样多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂利用辐射对食品进行灭菌消毒,现准备在该厂附近建一职工宿舍,并对宿舍进行防辐射处理,建房防辐射材料的选用与宿舍到工厂距离有关.若建造宿舍的所有费用![]() (万元)和宿舍与工厂的距离
(万元)和宿舍与工厂的距离![]() 的关系为:
的关系为: ![]() .为了交通方便,工厂与宿舍之间还要修一条简易便道,已知修路每公里成本为
.为了交通方便,工厂与宿舍之间还要修一条简易便道,已知修路每公里成本为![]() 万元,工厂一次性补贴职工交通费
万元,工厂一次性补贴职工交通费![]() 万元.设
万元.设![]() 为建造宿舍、修路费用与给职工的补贴之和.
为建造宿舍、修路费用与给职工的补贴之和.
⑴求![]() 的表达式;
的表达式;
⑵宿舍应建在离工厂多远处,可使总费用![]() 最小,并求最小值.
最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列A: ![]() ,
, ![]() ,…
,… ![]() (N≥2)。如果对小于n(2≤n≤N)的每个正整数k都有
(N≥2)。如果对小于n(2≤n≤N)的每个正整数k都有 ![]() <
< ![]() ,则称n是数列A的一个“G时刻”。记“G(A)是数列A 的所有“G时刻”组成的集合。
,则称n是数列A的一个“G时刻”。记“G(A)是数列A 的所有“G时刻”组成的集合。
(1)对数列A:-2,2,-1,1,3,写出G(A)的所有元素;
(2)证明:若数列A中存在 ![]() 使得
使得 ![]() >
> ![]() ,则G(A)
,则G(A) ![]()
![]() ;
;
(3)证明:若数列A满足 ![]() -
- ![]() ≤1(n=2,3, …,N),则GA.的元素个数不小于
≤1(n=2,3, …,N),则GA.的元素个数不小于 ![]() -
- ![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选做题】本题包括A、B、C、D四小题,请选定其中两小题,并在相应的答题区域内作答.若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.
(1)A.【选修4—1几何证明选讲】
如图,在△ABC中,∠ABC=90°,BD⊥AC , D为垂足,E是BC的中点,求证:∠EDC=∠ABD.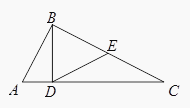
(2)B.【选修4—2:矩阵与变换】
已知矩阵A= ![]() 矩阵B的逆矩阵B﹣1=
矩阵B的逆矩阵B﹣1= 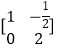 ,求矩阵AB.
,求矩阵AB.
(3)【选修4—4:坐标系与参数方程】在平面直角坐标系xOy中,已知直线l的参数方程为 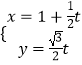 (t为参数),椭圆C的参数方程为
(t为参数),椭圆C的参数方程为 ![]() (
( ![]() 为参数).设直线l与椭圆C相交于A , B两点,求线段AB的长.
为参数).设直线l与椭圆C相交于A , B两点,求线段AB的长.
(4)D. 设a>0,|x﹣1|< ![]() ,|y﹣2|<
,|y﹣2|< ![]() ,求证:|2x+y﹣4|<a.
,求证:|2x+y﹣4|<a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海关对同时从![]() 三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示,工作人员用分层抽样的方法从这些商品中共抽取6件进行检测.
三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示,工作人员用分层抽样的方法从这些商品中共抽取6件进行检测.
地区 |
|
|
|
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自![]() 各地区商品的数量;
各地区商品的数量;
(2)若在这6件样品中随机抽取2件送往甲机构进一步检测,求这2件商品来自相同地区的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com