练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设是公比为q的等比数列.

    (Ⅰ) 推导的前n项和公式;

    (Ⅱ) 设q≠1, 证明数列不是等比数列.

    【答案】(Ⅰ)见解析；(Ⅱ)见解析

    【解析】

    （Ⅰ）设等比数列的公比为q，其前n项和为（1）

    将（1）式两边分别乘以q得

    （2）

    （1）-（2）得

    当时或

    当时，，所以

    （Ⅱ）方法一：

    均与题设矛盾，故数列不可能为等比数列.

    方法二：

    均与题设矛盾，故数列不可能为等比数列.

    本题考查了等比数列前项和公式的推导，涉及参数q分类讨论及错位相减法，体现高考题型源于教材的基本理念.而在第二问中要求证明数列不是等比数列，既考查了对等比数列概念的理解，又涉及到了反证法的应用；知识有机结合，考查综合能力.问中对数列的证明可以采取特殊代替一般的方法，也可以通行通法的解题思想.判断一个数列是否是等比数列一定要关注首项的验证，负责容易错误.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】将正方形沿对角线折叠，使平面平面， 若直线平面，，．

    求证：直线平面；

    求三棱锥的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】有2008名学生参加大型公益活动．若有两名学生互相认识，则将这两名学生看作一个合作小组．

    （1）求合作小组数目的最小值，使得无论学生认识的情况如何，都存在三名学生，他们两两都在一个合作小组；

    （2）若合作小组数目为，证明：存在四名学生、、、，使得和、和、和、和分别为一个合作小组．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】任意给定一个大于1的整数n，试设计一个程序或步骤对n是否为素数作出判断.算法：第一步：判断n是否等于2.若______，则_______；若______，则执行第二步；第二步：依次从_______是不是n的因数，若有_________，则n不是_________数；若_______，则n____________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设等比数列的公比为，前项和.

    （1）求的取值范围；

    （2）设，记的前项和为，试比较与的大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线.

    （1）若过点作与抛物线相交的弦，要使其弦长为2的弦有几条？并说明理由.

    （2）试研究过点，且使弦长为2的弦有几条？并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点O为坐标原点，椭圆C：（a＞b＞0）的左、右焦点分别为F1，F2，离心率为，点I，J分别是椭圆C的右顶点、上顶点，△IOJ的边IJ上的中线长为．

    （1）求椭圆C的标准方程；

    （2）过点H（－2，0）的直线交椭圆C于A，B两点，若AF1⊥BF1，求直线AB的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】全民健身倡导全民做到每天参加一次以上的体育健身活动，旨在全面提高国民体质和健康水平.某市的体育部门对某小区的4000人进行了“运动参与度”统计评分（满分100分），得到了如下的频率分布直方图：

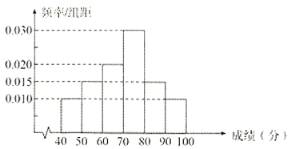
    （1）求这4000人的“运动参与度”的平均得分（同一组中数据用该组区间中点作代表）；

    （2）由直方图可认为这4000人的“运动参与度”的得分服从正态分布，其中，分别取平均得分和方差，那么选取的4000人中“运动参与度”得分超过84.81分（含84.81分）的人数估计有多少人？

    （3）如果用这4000人得分的情况来估计全市所有人的得分情况，现从全市随机抽取4人，记“运动参与度”的得分不超过84.81分的人数为，求.（精确到0.001）

    附：①，；②，则，；③.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如果不是等差数列，但若，使得，那么称为“局部等差”数列.已知数列的项数为4，记事件：集合，事件：为“局部等差”数列，则条件概率（ ）

    A. B. C. D.

    查看答案和解析>>

    同步练习册答案