
【题目】如图(1),五边形PABCD是由一个正方形与一个等腰三角形拼接而成,其中∠APD=120°,AB=2,现将△PAD进行翻折,使得平面PAD⊥平面ABCD,连接PB,PC,所得四棱锥P﹣ABCD如图(2)所示,则四棱锥P﹣ABCD的外接球的表面积为( ) 
A.![]()
B.![]()
C.![]()
D.14π
【答案】C
【解析】解:将四棱锥P﹣ABCD补成直三棱柱PAD﹣MBC, 则直三棱柱PAD﹣MBC与四棱锥P﹣ABCD的外接球是同一个球,
故只需求出直三棱柱PAD﹣MBC的外接球半径即可.
如图,设直三棱柱PAD﹣MBC的两底的外接圆圆心分别为O1 , O2 , 连接O1O2 , 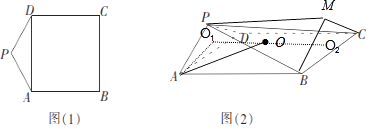
根据对称性球心为线段O1O2的中点O,
又∵底ADP的外接圆半径r,由正弦定理得 ![]() ,r=
,r= ![]() ,
,
直三棱柱PAD﹣MBC的外接球半径R= ![]() .
.
∴四棱锥P﹣ABCD的外接球的表面积为s=4πR2= ![]() .
.
故选:C.
【考点精析】掌握球内接多面体是解答本题的根本,需要知道球的内接正方体的对角线等于球直径;长方体的外接球的直径是长方体的体对角线长.


科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCDEF中,底面ABCD为正方形,平面AED⊥平面ABCD,AB= ![]() EA=
EA= ![]() ED,EF∥BD
ED,EF∥BD 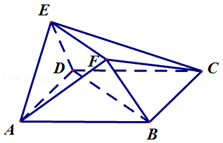
(I)证明:AE⊥CD
(II)在棱ED上是否存在点M,使得直线AM与平面EFBD所成角的正弦值为 ![]() ?若存在,确定点M的位置;若不存在,请说明理由.
?若存在,确定点M的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目.根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损分别为30%和10%.投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元.问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}中,若存在ak , 使得“ak>ak﹣1且ak>ak+1”成立(其中k≥2,k∈N*),则称ak为{an}的一个H值.现有如下数列:①an=1﹣2n;②an=sinn;③an= ![]() ④an=lnn﹣n,则存在H值的数列有( )个.
④an=lnn﹣n,则存在H值的数列有( )个.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中xOy,直线C1的参数方程为 ![]() (t是参数).在以坐标原点为极点,x轴非负半轴为极轴的极坐标系中,曲线C2的极坐标方程为ρ=sinθ﹣cosθ(θ是参数).
(t是参数).在以坐标原点为极点,x轴非负半轴为极轴的极坐标系中,曲线C2的极坐标方程为ρ=sinθ﹣cosθ(θ是参数).
(Ⅰ)将曲线C2的极坐标方程化为直角坐标方程,并判断曲线C2所表示的曲线;
(Ⅱ)若M为曲线C2上的一个动点,求点M到直线C1的距离的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣b)lnx+x2在区间[1,e]上单调递增,则实数b的取值范围是( )
A.(﹣∞,﹣3]
B.(﹣∞,2e]
C.(﹣∞,3]
D.(﹣∞,2e2+2e]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 f(x)=![]() ,其中 c>a>0,c>b>0.若 a,b,c 是△ABC 的三条边长,给出下列命题:
,其中 c>a>0,c>b>0.若 a,b,c 是△ABC 的三条边长,给出下列命题:
①对于x∈(-∞,1),都有 f(x)>0;
②存在 x>0,使![]() ,
,![]() ,
,![]() 不能构成一个三角形的三边长;
不能构成一个三角形的三边长;
③若△ABC 为钝角三角形,则存在 x∈(1,2),使 f(x)=0.
则其中所有正确结论的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高职院校进行自主招生文化素质考试,考试内容为语文、数学、英语三科,总分为200分.现从上线的考生中随机抽取20人,将其成绩用茎叶图记录如下:
男 | 女 | |||||||||||
15 | 6 | |||||||||||
5 | 4 | 16 | 3 | 5 | 8 | |||||||
8 | 2 | 17 | 2 | 3 | 6 | 8 | 8 | 8 | ||||
6 | 5 | 18 | 5 | 7 | ||||||||
19 | 2 | 3 | ||||||||||
(Ⅰ)计算上线考生中抽取的男生成绩的方差![]() ;(结果精确到小数点后一位)
;(结果精确到小数点后一位)
(Ⅱ)从上述茎叶图180分以上的考生中任选2人作为考生代表出席座谈会,求所选考生恰为一男一女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com