
【题目】已知函数![]()
![]() 若
若![]() 是函数
是函数![]() 的极值点,1是函数
的极值点,1是函数![]() 的一个零点,求
的一个零点,求![]() 的值;
的值;
![]() 当
当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
![]() 若对任意
若对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,求实数a的取值范围.
成立,求实数a的取值范围.
【答案】(1)![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() .
.
【解析】
(1)先求导得到![]() ,由
,由![]() ,
,![]() ,得到
,得到![]() 的值,继而求出
的值,继而求出![]() 的值;
的值;
(2)求出函数的导数,通过讨论![]() 的范围,求出函数的单调区间即可;
的范围,求出函数的单调区间即可;
(3)令![]() ,问题转化为
,问题转化为![]() 上
上![]() 有解即可,亦即只需存在
有解即可,亦即只需存在![]() 使得
使得![]() 即可,连续利用导函数,然后分别对
即可,连续利用导函数,然后分别对![]() ,看是否存在
,看是否存在![]() 使得
使得![]() ,进而得到结论.
,进而得到结论.
(1)![]() ,
,
∵![]() 是函数
是函数![]() 的极值点,
的极值点,
∴![]() .
.
∵1是函数![]() 的零点,得
的零点,得![]() ,
,
由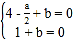 ,
,
解得![]() ,
,![]() ,
,
∴![]() ;
;
(2)![]() 时,
时,![]() ,
,![]() ,
,
![]() ,
,
![]() 时,
时,![]() ,
,![]() 递增,
递增,
![]() 时,令
时,令![]() ,解得:
,解得:![]() ,
,
令![]() ,解得:
,解得:![]() ,
,
故![]() 在
在![]() 递减,在
递减,在![]() 递增;
递增;
(3)令![]() ,
,![]() ,则
,则![]() 为关于
为关于![]() 的一次函数且为增函数,
的一次函数且为增函数,
根据题意,对任意![]() ,都存在
,都存在![]() (
(![]() 为自然对数的底数),使得
为自然对数的底数),使得![]() 成立,
成立,
则在![]() 上
上![]() ,有解,
,有解,
令![]() ,只需存在
,只需存在![]() 使得
使得![]() 即可,
即可,
由于![]() ,
,
令![]() ,
,![]() ,
,![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,
①当![]() ,即
,即![]() 时,
时,![]() ,即
,即![]() ,
,![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() ,不符合题意.
,不符合题意.
②当![]() ,即
,即![]() 时,
时,![]() ,
,![]()
若![]() ,则
,则![]() ,所以在
,所以在![]() 上
上![]() 恒成立,即
恒成立,即![]() 恒成立,∴
恒成立,∴![]() 在
在![]() 上单调递减,
上单调递减,
∴存在![]() 使得
使得![]() ,符合题意.
,符合题意.
若![]() ,则
,则![]() ,∴在
,∴在![]() 上一定存在实数
上一定存在实数![]() ,使得
,使得![]() ,
,
∴在![]() 上
上![]() 恒成立,即
恒成立,即![]() 恒成立,∴
恒成立,∴![]() 在
在![]() 上单调递减,
上单调递减,
∴存在![]() 使得
使得![]() ,符合题意.综上所述,当
,符合题意.综上所述,当![]() 时,对任意
时,对任意![]() ,都存在
,都存在![]() (
(![]() 为自然对数的底数),使得
为自然对数的底数),使得![]() 成立.
成立.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:
【题目】据气象中心观察和预测:发生于甲地的沙尘暴一直向正南方向移动,其移动速度![]() 与时间
与时间![]() 的函数图象图所示,过线段
的函数图象图所示,过线段![]() 上一点
上一点![]() 作横轴的垂线
作横轴的垂线![]() ,梯形
,梯形![]() 在直线
在直线![]() 左侧部分的面积即为
左侧部分的面积即为![]() 内沙尘暴所经过的路程
内沙尘暴所经过的路程![]() .
.
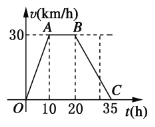
(1) 当![]() 时,求
时,求![]() 的值;
的值;
(2)将![]() 随
随![]() 变化的规律用数学关系式表示出来;
变化的规律用数学关系式表示出来;
(3)若乙城位于甲地正南方向,且距甲地![]() ,试判断这场沙尘暴是否会侵袭到乙城,如果会,在沙尘暴发生后多长时间它将侵袭到乙城?如果不会,请说明理由.
,试判断这场沙尘暴是否会侵袭到乙城,如果会,在沙尘暴发生后多长时间它将侵袭到乙城?如果不会,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法错误的是( )
A. 若“![]() ”为假命题,则p,q均为假命题
”为假命题,则p,q均为假命题
B. “ ![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
C. “![]() ”的必要不充分条件是“
”的必要不充分条件是“![]() ”
”
D. 若命题p:![]() ,
,![]() ,则命题
,则命题![]() :
:![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中“sinA>sinB”是“cosA<cosB”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知倾斜角为![]() 的直线
的直线![]() 过点
过点![]() 和点
和点![]() ,点
,点![]() 在第一象限,
在第一象限,![]() .
.
(1)求![]() 的坐标;
的坐标;
(2)若直线![]() 与两平行直线
与两平行直线![]() ,
,![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值;
的值;
(3)记集合![]() 直线
直线![]() 经过点
经过点![]() 且与坐标轴围成的面积为
且与坐标轴围成的面积为![]() ,
,![]() ,针对
,针对![]() 的不同取值,讨论集合
的不同取值,讨论集合![]() 中的元素个数.
中的元素个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点M(0,2),N(-2,0),直线l:kx-y-2k+2=0(k为常数).
(1)若点M,N到直线l的距离相等,求实数k的值;
(2)对于l上任意一点P,∠MPN恒为锐角,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com