
【题目】已知函数 ![]() 在(1,+∞)上是增函数,且a>0.
在(1,+∞)上是增函数,且a>0.
(Ⅰ)求a的取值范围;
(Ⅱ)求函数g(x)=ln(1+x)﹣x在[0,+∞)上的最大值;
(Ⅲ)已知a>1,b>0,证明: ![]() .
.
【答案】解:(Ⅰ)f(x)的导数为 ![]() ,
,
因为函数f(x)在(1,+∞)上是增函数,
所以 ![]() ≥0在(1,+∞)上恒成立,
≥0在(1,+∞)上恒成立,
即 ![]() 在(1,+∞)上恒成立,
在(1,+∞)上恒成立,
所以只需 ![]() ,
,
又因为a>0,所以a≥1.
(Ⅱ)因为x∈[0,+∞),所以 ![]() ,
,
所以g(x)在[0,+∞)上单调递减,
所以g(x)=ln(1+x)﹣x在[0,+∞)上的最大值为g(0)=0.
(Ⅲ)证明:因为a>1,b>0,所以 ![]() ,由(Ⅰ)知
,由(Ⅰ)知 ![]() 在(1,+∞)上是增函数,
在(1,+∞)上是增函数,
所以 ![]() ,即
,即 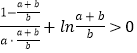 ,化简得
,化简得 ![]() ,又因为
,又因为 ![]() ,
,
由第(Ⅱ)问可知 ![]() ,即
,即 ![]() ,
,
综上 ![]() 得证
得证
【解析】(Ⅰ)求导,由题意可知 ![]() ≥0在(1,+∞)上恒成立,则即可求得a的取值范围;(Ⅱ)由
≥0在(1,+∞)上恒成立,则即可求得a的取值范围;(Ⅱ)由 ![]() ,则g(x)在[0,+∞)上单调递减,求得g(x)最大值;(Ⅲ)由(Ⅰ)知
,则g(x)在[0,+∞)上单调递减,求得g(x)最大值;(Ⅲ)由(Ⅰ)知 ![]() 在(1,+∞)上是增函数,则
在(1,+∞)上是增函数,则 ![]() ,化简得
,化简得 ![]() ,由(Ⅱ)可知
,由(Ⅱ)可知 ![]() ,即
,即 ![]() .
.
【考点精析】根据题目的已知条件,利用利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识可以得到问题的答案,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


科目:高中数学 来源: 题型:
【题目】设M,N为两个随机事件,给出以下命题: (1.)若M、N为互斥事件,且 ![]() ,
, ![]() ,则
,则 ![]() ;
;
(2.)若 ![]() ,
, ![]() ,
, ![]() ,则M、N为相互独立事件;
,则M、N为相互独立事件;
(3.)若 ![]() ,
, ![]() ,
, ![]() ,则M、N为相互独立事件;
,则M、N为相互独立事件;
(4.)若 ![]() ,
, ![]() ,
, ![]() ,则M、N为相互独立事件;
,则M、N为相互独立事件;
(5.)若 ![]() ,
, ![]() ,
, ![]() ,则M、N为相互独立事件;
,则M、N为相互独立事件;
其中正确命题的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在常数k(k∈N* , k≥2)、q、d,使得无穷数列{an}满足  则称数列{an}为“段比差数列”,其中常数k、q、d分别叫做段长、段比、段差.设数列{bn}为“段比差数列”.
则称数列{an}为“段比差数列”,其中常数k、q、d分别叫做段长、段比、段差.设数列{bn}为“段比差数列”.
(1)若{bn}的首项、段长、段比、段差分别为1、3、q、3. ①当q=0时,求b2016;
②当q=1时,设{bn}的前3n项和为S3n , 若不等式 ![]() 对n∈N*恒成立,求实数λ的取值范围;
对n∈N*恒成立,求实数λ的取值范围;
(2)设{bn}为等比数列,且首项为b,试写出所有满足条件的{bn},并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知x1 , x2是方程e﹣x+2=|lnx|的两个解,则( )
A.0<x1x2< ![]()
B.![]() <x1x2<1
<x1x2<1
C.1<x1x2<e
D.x1x2>e
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为得到函数y=2cos2x﹣ ![]() sin2x的图象,只需将函数y=2sin2x+1的图象( )
sin2x的图象,只需将函数y=2sin2x+1的图象( )
A.向左平移 ![]() 个长度单位
个长度单位
B.向右平移 ![]() 个长度单位
个长度单位
C.向左平移 ![]() 个长度单位
个长度单位
D.向右平移 ![]() 个长度单位
个长度单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=lnx﹣ax2+ax,a为正实数.
(1)当a=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求证:f( ![]() )≤0;
)≤0;
(3)若函数f(x)有且只有1个零点,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,矩形ABCD中,AB=1,AD=2,点E为AD中点,沿BE将△ABE折起至△PBE,如图2所示,点P在面BCDE的射影O落在BE上. 
(Ⅰ)求证:BP⊥CE;
(Ⅱ)求二面角B﹣PC﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个酒杯的轴截面是一条抛物线的一部分,它的方程是x2=2y,y∈[0,10],在杯内放入一个清洁球,要求清洁球能擦净酒杯的最底部(如图),则清洁球的最大半径为 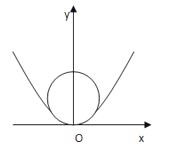
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com