
【题目】为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
是否需要志愿 性别 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
 附:
附:
【答案】![]() ,有99%的把握认为该地区的老年人是否需要帮助与性别有关
,有99%的把握认为该地区的老年人是否需要帮助与性别有关
该地区老年人是否需要帮助与性别有关,并且从样本数据能看出该地区男性老年人与女性老年人中需要帮助的比例有明显差异,因此在调查时,先确定该地区老年人中男、女的比例,再把老年人分成男、女两层并采用分层抽样方法比采用简单随机抽样方法更好.
【解析】(1)调查的500位老年人中有70位需要志愿者提供帮助,因此该地区老年人中,需要帮助的老年人的比例的估算值为![]()
(2)![]() 。
。
由于9.967>6.635,所以有99%的把握认为该地区的老年人是否需要帮助与性别有关。
(III)由(II)的结论知,该地区老年人是否需要帮助与性别有关,并且从样本数据能看出该地区男性老年人与女性老年人中需要帮助的比例有明显差异,因此在调查时,先确定该地区老年人中男、女的比例,再把老年人分成男、女两层并采用分层抽样方法比采用简单随机抽样方法更好.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是定义在R上的偶函数,对于x∈R,都有f(x+4)=f(x)+f(2)成立,当x1 , x2∈[0,2]且x1≠x2时,都有 ![]() <0,给出下列四个命题:
<0,给出下列四个命题:
①f(﹣2)=0;
②直线x=﹣4是函数y=f(x)的图象的一条对称轴;
③函数y=f(x)在[4,6]上为增函数;
④函数y=f(x)在(﹣8,6]上有四个零点.
其中所有正确命题的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)若函数f(x)在区间(a,a+ ![]() )(a>0)上存在极值点,求实数a的取值范围;
)(a>0)上存在极值点,求实数a的取值范围;
(2)当x≥1时,不等式f(x)≥ ![]() 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+ax2+bx,(a,b∈R).
(1)设a=1,f(x)在x=1处的切线过点(2,6),求b的值;
(2)设b=a2+2,求函数f(x)在区间[1,4]上的最大值;
(3)定义:一般的,设函数g(x)的定义域为D,若存在x0∈D,使g(x0)=x0成立,则称x0为函数g(x)的不动点.设a>0,试问当函数f(x)有两个不同的不动点时,这两个不动点能否同时也是函数f(x)的极值点?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形.点E是棱PC的中点,平面ABE与棱PD交于点F.
(Ⅰ)求证:AB∥EF;
(Ⅱ)若PA=AD,且平面PAD⊥平面ABCD,求证:AF⊥平面PCD.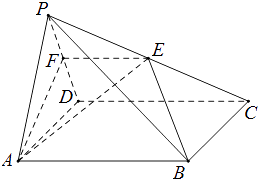
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】环保部门对5家造纸厂进行排污检查,若检查不合格,则必须整改,整改后经复查仍然不合格的,则关闭.设每家造纸厂检查是否合格是相互独立的,且每家造纸厂检查前合格的概率是 ![]() ,整改后检查合格的概率是
,整改后检查合格的概率是 ![]() ,求:
,求:
(Ⅰ)恰好有两家造纸厂必须整改的概率;
(Ⅱ)至少要关闭一家造纸厂的概率;
(Ⅲ)平均多少家造纸厂需要整改?(其中( ![]() )5≈
)5≈ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某宾馆在装修时,为了美观,欲将客房的窗户设计成半径为1m的圆形,并用四根木条将圆分成如图所示的9个区域,其中四边形ABCD为中心在圆心的矩形,现计划将矩形ABCD区域设计为可推拉的窗口. 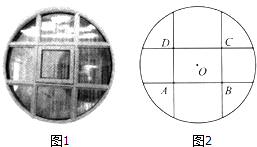
(1)若窗口ABCD为正方形,且面积大于 ![]() m2(木条宽度忽略不计),求四根木条总长的取值范围;
m2(木条宽度忽略不计),求四根木条总长的取值范围;
(2)若四根木条总长为6m,求窗口ABCD面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com