
已知![]()
(Ⅰ)若![]() 求
求![]() 的表达式;
的表达式;
(Ⅱ)若函数f (x)和函数g(x)的图象关于原点对称,求函数g(x)的解析式;
(Ⅲ)若![]() 在
在![]() 上是增函数,求实数l的取值范围
上是增函数,求实数l的取值范围
(Ⅰ) ![]() = sin2x+2sinx(Ⅱ)g(x)= -sin2x+2sinx(Ⅲ)
= sin2x+2sinx(Ⅱ)g(x)= -sin2x+2sinx(Ⅲ)![]()
(1)![]()
=2+sinx-cos2x-1+sinx=sin2x+2sinx
(1)设函数y=f (x)的图象上任一点M(x0,y0)关于原点的对称点为N(x,y)
则x0= -x,y0= -y
∵点M在函数y=f (x)的图象上
![]() ,即y= -sin2x+2sinx
,即y= -sin2x+2sinx
∴函数g(x)的解析式为g(x)= -sin2x+2sinx
(3)![]() 设sinx=t,(-1≤t≤1)
设sinx=t,(-1≤t≤1)
则有![]()
当![]() 时,h(t)=4t+1在[-1,1]上是增函数,∴λ= -1
时,h(t)=4t+1在[-1,1]上是增函数,∴λ= -1
当![]() 时,对称轴方程为直线
时,对称轴方程为直线![]() .
.
ⅰ) ![]() 时,
时,![]() ,解得
,解得![]()
ⅱ)当![]() 时,
时,![]() ,解得
,解得![]()
综上,![]() .
.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:
| 喜爱程度 | 喜欢 | 一般 | 不喜欢 |
| 人数 | 560 | 240 | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:
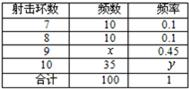
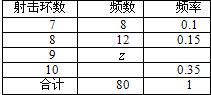
查看答案和解析>>
科目:高中数学 来源: 题型:
已知10只狗的血球体积及红血球的测量值如下
|
|
|
| 45 | 6.53 |
| 42 | 6.30 |
| 46 | 9.25 |
| 48 | 7.50 |
| 42 | 6.99 |
| 35 | 5.90 |
| 58 | 9.49 |
| 40 | 6.20 |
| 39 | 6.55 |
| 50 | 7.72 |
![]() (血球体积,mm),
(血球体积,mm),![]() (红血球数,百万)
(红血球数,百万)
(1) 画出上表的散点图;
(2)求出回归直线并且画出图形;
(3)若血球体积为49mm,预测红血球数大约是多少?
查看答案和解析>>
科目:高中数学 来源:2011届广东省高考猜押题卷文科数学(三)解析版 题型:解答题
(本小题满分12分)
第26届世界大学生夏季运动会将于2011年8月12日到23日在深圳举行,为了搞好接待工作,组委会决定对礼仪小姐进行培训.已知礼仪小姐培训班的项目A与项目B成绩抽样统计表如下,抽出礼仪小姐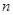 人,成绩只有
人,成绩只有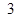 、
、 、
、 三种分值,设
三种分值,设 分别表示项目A与项目B成绩.例如:表中项目A成绩为
分别表示项目A与项目B成绩.例如:表中项目A成绩为 分的共7+9+4=20人.已知
分的共7+9+4=20人.已知 且
且 的概率是
的概率是 .
.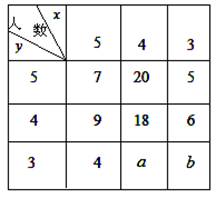
(I)求 ;
;
(II)若在该样本中,再按项目B的成绩分层抽样抽出 名礼仪小姐,则
名礼仪小姐,则 的礼仪小姐中应抽多少人?
的礼仪小姐中应抽多少人?
(Ⅲ)已知 ,
, ,项目B为3分的礼仪小姐中,求项目A得3分的人数比得4分人数多的概率.
,项目B为3分的礼仪小姐中,求项目A得3分的人数比得4分人数多的概率.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省南阳市高三春期第十一次考试理科数学试卷(解析版) 题型:解答题
已知椭圆 、抛物线
、抛物线 的焦点均在
的焦点均在 轴上,
轴上, 的中心和
的中心和 的顶点均为原点
的顶点均为原点 ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
|
|
3 |
|
4 |
|
|
|
|
0 |
|
|
(1)求 ,
, 的标准方程;
的标准方程;
(2)请问是否存在直线 满足条件:①过
满足条件:①过 的焦点
的焦点 ;②与
;②与 交于不同两点
交于不同两点 ,
, ,且满足
,且满足 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com