
【题目】已知三棱锥![]() 中,
中,![]() 面
面![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,则该三棱锥的外接球的表面积为__________.
,则该三棱锥的外接球的表面积为__________.
【答案】![]()
【解析】
根据题意,证出BC⊥平面SAC,可得BC⊥SC,得Rt△BSC的中线OC![]() SB,同理得到OA
SB,同理得到OA![]() SB,因此O是三棱锥S﹣ABC的外接球心.利用勾股定理结合题中数据算出SC,得外接球半径R=
SB,因此O是三棱锥S﹣ABC的外接球心.利用勾股定理结合题中数据算出SC,得外接球半径R=![]() ,从而得到所求外接球的表面积.
,从而得到所求外接球的表面积.
取SB的中点O,连结OA、OC
∵SA⊥平面ABC,AB平面ABC,
∴SA⊥AB,可得Rt△ASB中,中线OA![]() SB
SB
由![]() ,
,![]() ,
,![]() ,可知:AC⊥BC,
,可知:AC⊥BC,
又∵SA⊥BC, SA、AB是平面SAB内的相交直线
∴BC⊥平面SAC,可得BC⊥SC
因此Rt△BSC中,中线OC![]() SB
SB
∴O是三棱锥S﹣ABC的外接球心,
∵Rt△SBA中,AB![]() ,SA=6
,SA=6
∴SB=2,可得外接球半径R![]() SB=
SB=![]()
因此,外接球的体积S![]() Πr2
Πr2![]() π
π
故答案为:![]() π.
π.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:
【题目】某贫困地区共有1500户居民,其中平原地区1050户,山区450户.为调查该地区2017年家庭收入情况,从而更好地实施“精准扶贫”,采用分层抽样的方法,收集了150户家庭2017年年收入的样本数据(单位:万元).

(1)应收集多少户山区家庭的样本数据?
(2)根据这150个样本数据,得到2017年家庭收入的频率分布直方图(如图所示),其中样本数据分组区间为(0,0.5],(0.5,1],(1,1.5],(1.5,2],(2,2.5],(2.5,3].如果将频率视为概率,估计该地区2017年家庭收入超过1.5万元的概率;
(3)样本数据中,有5户山区家庭的年收入超过2万元,请完成2017年家庭收入与地区的列联表,并判断是否有90%的把握认为“该地区2017年家庭年收入与地区有关”?
超过2万元 | 不超过2万元 | 总计 | |
平原地区 | |||
山区 | 5 | ||
总计 |
附:
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和
项和![]() 满足:
满足:![]() (
(![]() 为常数,且
为常数,且![]() ,
,![]() ).
).
(1)求![]() 的通项公式;
的通项公式;
(2)设![]() ,若数列
,若数列![]() 为等比数列,求
为等比数列,求![]() 的值;
的值;
(3)在满足条件(2)的情形下,设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,若不等式
,若不等式![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,过右焦点
,过右焦点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,
两点,![]() 的周长为
的周长为![]() ,点
,点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 、
、![]() 的斜率
的斜率![]() ,
,![]() ,请问
,请问![]() 是否为定值?若是定值,求出其定值;若不是,说明理由.
是否为定值?若是定值,求出其定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
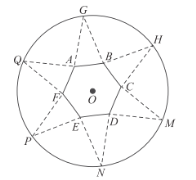
【题目】如图,圆形纸片的圆心为O,半径为5cm,该纸片上的正六边形ABCDEF的中心为O,G、H、M、N、P、Q为圆O上的点,△GAB,△HBC,△MCD,△NDE,△PEF,△QAF分别是以AB,BC,CD,DE,EF,FA为底边的等腰三角形,沿虚线剪开后,分别以AB,BC,CD,DE,EF,FA为折痕折起△GAB,△HBC,△MCD,△NDE,△PEF,△QAF,使得G、H、M、N、P、Q重合,得到六棱锥.当正六边形ABCDEF的边长变化时,所得六棱锥体积(单位:cm3)的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】疫情期间,有一批货物需要用汽车从城市甲运至城市乙,已知从城市甲到城市乙只有两条公路,且通过这两条公路所用的时间互不影响.据调查统计,通过这两条公路从城市甲到城市乙的200辆汽车所用时间的频数分布如下表:
所用时间 | 10 | 11 | 12 | 13 |
通过公路1的频数 | 20 | 40 | 20 | 20 |
通过公路2的频数 | 10 | 40 | 40 | 10 |
(1)为进行某项研究,从所用时间为12的60辆汽车中随机抽取6辆,若用分层随机抽样的方法抽取,求从通过公路1和公路2的汽车中各抽取几辆:
(2)若从(1)的条件下抽取的6辆汽车中,再任意抽取2辆汽车,求这2辆汽车至少有1辆通过公路1的概率;
(3)假设汽车A只能在约定时间的前11h出发,汽车B只能在约定时间的前12h出发.为了尽最大可能在各自允许的时间内将货物从城市甲运到城市乙,汽车A和汽车B应如何选择各自的道路?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com