
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形,![]() 平面
平面![]() ,
,![]() 为
为![]() 的中点.
的中点.
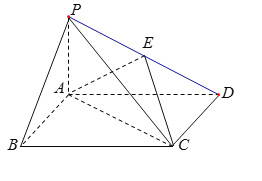
(1)证明:![]() ∥平面
∥平面![]() .
.
(2)设二面角![]() 为
为![]() ,
,![]() ,
,![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析(2)![]()
【解析】
(1)连结![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() . 根据四边形
. 根据四边形![]() 为矩形,所以
为矩形,所以![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,利用三角形的中位线可得
的中点,利用三角形的中位线可得![]() ∥
∥![]() ,再利用线面平行的判定定理证明.
,再利用线面平行的判定定理证明.
(2) 根据![]() 平面
平面![]() ,四边形
,四边形![]() 为矩形,建立空间直角坐标系
为矩形,建立空间直角坐标系![]() .设
.设![]() ,再求得平面DAE, 平面CAE的法向量,根据二面角
,再求得平面DAE, 平面CAE的法向量,根据二面角![]() 为
为![]() ,利用
,利用![]() ,解得
,解得![]() .,然后利用锥体体积公式求解.
.,然后利用锥体体积公式求解.
(1)连结![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() .
.
因为四边形![]() 为矩形,所以
为矩形,所以![]() 为
为![]() 的中点,
的中点,
又![]() 为
为![]() 的中点,所以
的中点,所以![]() ∥
∥![]() ,
,
且![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ∥平面
∥平面![]() .
.
(2) 因为![]() 平面
平面![]() ,四边形
,四边形![]() 为矩形,所以
为矩形,所以![]() 两两垂直,
两两垂直,
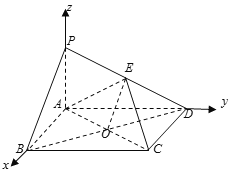
以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴的正方向,
轴的正方向,![]() 的方向为
的方向为![]() 轴的正方向,
轴的正方向,![]() 的方向为
的方向为![]() 轴的正方向,
轴的正方向,![]() 为单位长,建立空间直角坐标系
为单位长,建立空间直角坐标系![]() .
.
设![]() ,则
,则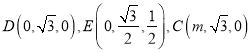 ,
,
所以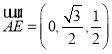 ,
,![]()
设![]() 为平面
为平面![]() 的法向量,则
的法向量,则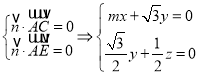 ,
,
可取![]() ,
,
又![]() 为平面
为平面![]() 的一个法向量,由题设知
的一个法向量,由题设知![]()
即![]() ,解得
,解得![]() .
.
因为![]() 为
为![]() 的中点,设
的中点,设![]() 为
为![]() 的中点,
的中点,
则![]() ∥
∥![]() ,且
,且![]() ,
,![]() ⊥面
⊥面![]() ,
,
故有三棱锥![]() 的高为
的高为![]() ,
,
三棱锥![]() 的体积
的体积![]()
所以三棱锥![]() 的体积为
的体积为![]() .
.


科目:高中数学 来源: 题型:
【题目】从一批苹果中随机抽取50个,其质量(单位:![]() )的频数分布表如下:
)的频数分布表如下:
分组 |
|
|
|
|
频数 | 5 | 10 | 20 | 15 |
用分层随机抽样的方法从质量在![]() 和
和![]() 内的苹果中共抽取4个,再从抽取的4个苹果中任取2个,则有1个苹果的质量在
内的苹果中共抽取4个,再从抽取的4个苹果中任取2个,则有1个苹果的质量在![]() 内的概率为( )
内的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() ,点
,点![]() 在直线
在直线![]() 上.
上.
(1)求数列![]() ,
,![]() 的通项公式
的通项公式![]() ,
,![]() ;
;
(2)令![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若![]() ,对所有的正整数
,对所有的正整数![]() 都有
都有![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,不等式
,不等式![]() 对
对![]() 恒成立.
恒成立.
(1)求函数![]() 的极值和函数
的极值和函数![]() 的图象在点
的图象在点![]() 处的切线方程;
处的切线方程;
(2)求实数![]() 的取值的集合
的取值的集合![]() ;
;
(3)设![]() ,函数
,函数![]() ,
,![]() ,其中
,其中![]() 为自然对数的底数,若关于
为自然对数的底数,若关于![]() 的不等式
的不等式![]() 至少有一个解
至少有一个解![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线![]() 的参数方程为
的参数方程为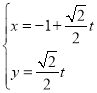 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与曲线C交于
与曲线C交于![]() 两点.
两点.
(1)求直线![]() 的普通方程和曲线C的直角坐标方程;
的普通方程和曲线C的直角坐标方程;
(2)求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com