
【题目】已知函数f(x)= ![]() ,g(x)=﹣2xln(1+
,g(x)=﹣2xln(1+ ![]() )﹣lnf(x).
)﹣lnf(x).
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)当a=0时,函数g(x)在定义域内是否存在零点?如果存在,求出该零点;如果不存在,请说明理由.
【答案】解:(Ⅰ)函数f(x)的定义域为R,f′(x)= 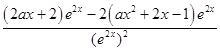 =
= ![]() =
= ![]()
①a=0时,f(′(x)=2× ![]() ,可得x∈(﹣∞,1)时,f′(x)>0,x∈(1,+∞),f′(x)<0,
,可得x∈(﹣∞,1)时,f′(x)>0,x∈(1,+∞),f′(x)<0,
此时f(x)在(﹣∞,1)递增,在(1,+∞)递减.
②a>0时,令f′(x)=0,x=1或x=﹣ ![]() ,可得x∈(﹣
,可得x∈(﹣ ![]() ,1)时,f′(x)>0,x∈(1,+∞)∪(﹣∞,﹣
,1)时,f′(x)>0,x∈(1,+∞)∪(﹣∞,﹣ ![]() ),f′(x)<0,
),f′(x)<0,
此时f(x)在(﹣ ![]() ,1)递增,在(﹣
,1)递增,在(﹣ ![]() ),(1,+∞)递减.
),(1,+∞)递减.
③a<0时,令f′(x)=0,x=1或x=﹣ ![]() ,
,
0>a>﹣2时,﹣ ![]() ,此时f(x)在(﹣∞,1),(﹣
,此时f(x)在(﹣∞,1),(﹣ ![]() )递增,在(1,﹣
)递增,在(1,﹣ ![]() )递减.
)递减.
a<﹣2时,1 ![]() ,此时f(x)在(﹣∞,﹣
,此时f(x)在(﹣∞,﹣ ![]() ),(1,+∞)递增,在(﹣
),(1,+∞)递增,在(﹣ ![]() ,1)递减.
,1)递减.
a=﹣2时.此时f(x)在(﹣∞,+∞)递增.
(Ⅱ)当a=0时,函数g(x)在定义域内不存在零点,理由如下:
a=0时,函数g(x)=﹣2xln ![]() ﹣ln
﹣ln ![]() =﹣2xln(x+1)+2xlnx﹣ln
=﹣2xln(x+1)+2xlnx﹣ln ![]() ,(x>
,(x> ![]() ).
).
函数g(x)在定义域内是否存在零点函数G(x)=﹣2xln(x+1)+2xlnx与R(x)=ln ![]() ,(x>
,(x> ![]() )是否有交点.
)是否有交点.
一方面:由(Ⅰ)知y= ![]() 在(﹣∞,1)递增,在(1,+∞)递减,可得R(x)=ln
在(﹣∞,1)递增,在(1,+∞)递减,可得R(x)=ln ![]() ,(x>
,(x> ![]() )在(
)在( ![]() ,1)递增,在(1,+∞)递减
,1)递增,在(1,+∞)递减
且x→ ![]() ,R(x)→﹣∞,x→+∞,R(x)→﹣∞,R(1)=﹣2<0
,R(x)→﹣∞,x→+∞,R(x)→﹣∞,R(1)=﹣2<0
另一方面:G′(x)=2[lnx﹣ln(x+1)+ ![]() ],G″(x)=2[
],G″(x)=2[ ![]() ﹣
﹣ ![]() ]>0在(
]>0在( ![]() )恒成立.
)恒成立.
∴G′(x)在( ![]() )递增,而G′(
)递增,而G′( ![]() )=2(﹣ln3+
)=2(﹣ln3+ ![]() )<0,x→+∞时,G(x)→0,∴G′(x)<0.
)<0,x→+∞时,G(x)→0,∴G′(x)<0.
∴函数G(x)在( ![]() )递减,G(
)递减,G( ![]() )=﹣ln3<0.
)=﹣ln3<0.
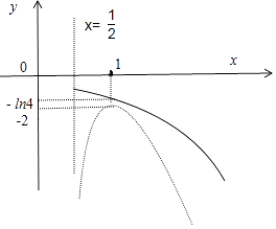
由此可以在同一坐标系画出两函数,如下:
结合图象可得,当a=0时,函数g(x)在定义域内不存在零点
【解析】(Ⅰ)函数f(x)的定义域为R,f′(x)= ![]() ,分①a=0,②a>0,③a<0讨论其单调性.(Ⅱ)a=0时,函数g(x)=﹣2xln
,分①a=0,②a>0,③a<0讨论其单调性.(Ⅱ)a=0时,函数g(x)=﹣2xln ![]() ﹣ln
﹣ln ![]() =﹣2xln(x+1)+2xlnx﹣ln
=﹣2xln(x+1)+2xlnx﹣ln ![]() (x>
(x> ![]() ),函数g(x)在定义域内是否存在零点函数G(x)=﹣2xln(x+1)+2xlnx与R(x)=ln
),函数g(x)在定义域内是否存在零点函数G(x)=﹣2xln(x+1)+2xlnx与R(x)=ln ![]() ,(x>
,(x> ![]() )是否有交点.分别讨论两函数的单调性,画出图象,结合图象求解.
)是否有交点.分别讨论两函数的单调性,画出图象,结合图象求解.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的极值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() 的左、右焦点分别为F1 , F2 , 左、右顶点分别为A,B.以F1F2为直径的圆O过椭圆E的上顶点D,直线DB与圆O相交得到的弦长为
的左、右焦点分别为F1 , F2 , 左、右顶点分别为A,B.以F1F2为直径的圆O过椭圆E的上顶点D,直线DB与圆O相交得到的弦长为 ![]() .设点P(a,t)(t≠0),连接PA交椭圆于点C,坐标原点为O.
.设点P(a,t)(t≠0),连接PA交椭圆于点C,坐标原点为O.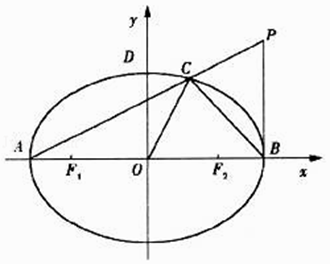
(I)求椭圆E的方程;
(II)若三角形ABC的面积不大于四边形OBPC的面积,求|t|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=  ,若a,b,c互不相等,且f(a)=f(b)=f(c),则a+b+c的取值范围是( )
,若a,b,c互不相等,且f(a)=f(b)=f(c),则a+b+c的取值范围是( )
A.(4,2018)
B.(4,2020)
C.(3,2020)
D.(2,2020)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒中装有编号分别为1,2,3,4的四个形状大小完全相同的小球.
(1)从盒中任取两球,求取出的球的编号之和大于5的概率.
(2)从盒中任取一球,记下该球的编号![]() ,将球放回,再从盒中任取一球,记下该球的编号
,将球放回,再从盒中任取一球,记下该球的编号![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且满足csinA=acosC
(1)求角C大小;
(2)求 ![]() sinA﹣cos(B+
sinA﹣cos(B+ ![]() )的最大值,并求取得最大值时角A,B的大小.
)的最大值,并求取得最大值时角A,B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC的三个内角A,B,C的三条对边,且c2=a2+b2﹣ab.
(Ⅰ)求角C的大小;
(Ⅱ)求cosA+cosB的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥ABCD﹣A1B1C1D1中,底面ABCD是等腰梯形,AB∥CD,AB=2,BC=CD=1,顶角D1在底面ABCD内的射影恰好为点C. 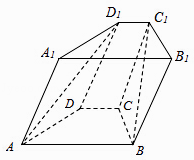
(1)求证:AD1⊥BC;
(2)若直线DD1与直线AB所成角为 ![]() ,求平面ABC1D1与平面ABCD所成角(锐角)的余弦值函数值.
,求平面ABC1D1与平面ABCD所成角(锐角)的余弦值函数值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图所示,在空间直角坐标系xOy平面内,若函数f(x)=  的图象与x轴围成一个封闭的区域A,将区域A沿z轴的正方向平移4个单位,得到几何体如图一,现有一个与之等高的圆柱如图二,其底面积与区域A的面积相等,则此圆柱的体积为 .
的图象与x轴围成一个封闭的区域A,将区域A沿z轴的正方向平移4个单位,得到几何体如图一,现有一个与之等高的圆柱如图二,其底面积与区域A的面积相等,则此圆柱的体积为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com