Question

【题目】已知复数z1=m+ni（m，n∈R），z=x+yi（x，y∈R），z2=2+4i且 ．
（1）若复数z1对应的点M（m，n）在曲线 上运动，求复数z所对应的点P（x，y）的轨迹方程；
（2）将（1）中的轨迹上每一点按向量 方向平移 个单位，得到新的轨迹C，求C的轨迹方程；
（3）过轨迹C上任意一点A（异于顶点）作其切线，交y轴于点B，求证：以线段AB为直径的圆恒过一定点，并求出此定点的坐标．

Answer 1

【答案】
（1）解：∵ i﹣z2=（m﹣ni）i﹣（2+4i）=（n﹣2）+（m﹣4）i；

∴ ．

∵复数z1对应的点M（m，n）在曲线 上运动

∴x+2=﹣ （y+7）2﹣1（y+7）2=﹣2（x+3）．

复数z所对应的点P（x，y）的轨迹方程：（y+7）2=﹣2（x+3）．

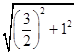（2）解：∵按向量 方向平移 个单位， = =1× ．

即为向 x 方向移动 1× = 个单位，向 y 方向移动 1×1=1 个单位

（y+7）2=﹣2（x+3）y+7=± ．

得轨迹方程 y+7=± 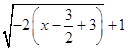（y+6）2=﹣2（x+ ）=﹣2x﹣3．

C的轨迹方程为：（y+6）2=﹣2x﹣3．

（3）解：设A（x0，y0），斜率为k，切线y﹣y0=k（x﹣x0） （k≠0），

代入（y+6）2=﹣2x﹣3整理得：

（y+6）2=﹣2（ ）﹣3，△=0k= ，

设定点M（1，0），且 ．

∴以线段AB为直径的圆恒过一定点M，M点的坐标（1，0）．

【解析】（1）根据复数条件求出关系式 ，结合复数z1对应的点M（m，n）在曲线 上运动即可得出复数z所对应的点P（x，y）的轨迹方程；（2）先按向量 方向平移 个单位得到即为向 x 方向移动 1× = 个单位，向 y 方向移动 1×1=1 个单位，再进行函数式的变换即可得出C的轨迹方程；（3）设A（x0，y0），斜率为k，切线y﹣y0=k（x﹣x0） 代入（y+6）2=﹣2x﹣3消去x得到关于y的一元二次方程，再结合根的判别式为0利用向量的数量即可求得定点，从而解决问题．