
| A. | p∧q | B. | p∨¬q | C. | ¬p∧q | D. | ¬p∧¬q |
分析 写出全程命题的否定判断p的真假;由函数零点存在性定理求出a的范围判断命题q的真假,然后由复合命题的真假判断逐一核对四个选项得答案.
解答 解:命题p:“?x>0,3x>1”的否定是“?x>0,3x≤1”,故命题p为假命题,¬p为真命题;
由函数f(x)=ax+3在区间[-1,2]上存在零点,得f(-1)f(2)≤0,
∴(-a+3)(2a+3)≤0,解得a≥3或$a≤-\frac{3}{2}$.
∴“a<-2”是“函数f(x)=ax+3在区间[-1,2]上存在零点”的充分不必要条件,故命题q为真命题,¬q为假命题.
故p∧q为假命题;p∨¬q为假命题;¬p∧q为真命题;¬p∧¬q为假命题.
故选:C.
点评 本题考查命题的真假判断与应用,考查了全程命题的否定,训练了函数零点存在性定理的应用方法,考查复合命题的真假判断,是基础题.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:解答题
| 规格类型 袋装大米类型 | A | B |
| 甲 | 2 | 1 |
| 乙 | 1 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 一天,小亮看到家中的塑料桶中有一个竖直放置的玻璃杯,桶子和玻璃杯的形状都是圆柱形,桶口的半径是杯口半径的2倍,其主视图如左图所示.小亮决定做个试验:把塑料桶和玻璃杯看作一个容器,对准杯口匀速注水,注水过程中杯子始终竖直放置,则下列能反映容器最高水位h与注水时间t之间关系的大致图象是( )
一天,小亮看到家中的塑料桶中有一个竖直放置的玻璃杯,桶子和玻璃杯的形状都是圆柱形,桶口的半径是杯口半径的2倍,其主视图如左图所示.小亮决定做个试验:把塑料桶和玻璃杯看作一个容器,对准杯口匀速注水,注水过程中杯子始终竖直放置,则下列能反映容器最高水位h与注水时间t之间关系的大致图象是( )| A. |  | B. |  | ||
| C. |  | D. | 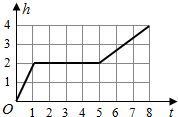 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若f(x)为增函数,g(x)为增函数,则f(x)+g(x)为增函数 | |
| B. | 若f(x)为减函数,g(x)为增函数,则f(x)-g(x)为减函数 | |
| C. | 若f(x)为奇函数,g(x)为偶函数,则f(x)-g(x)为奇函数 | |
| D. | 若f(x)为奇函数,g(x)为偶函数,则|f(x)|-g(x)为偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com