Question

设椭圆+y²=1的两个焦点是F₁（-c,0）与F₂（c,0）(c＞0),且椭圆上存在点M，使得·=0.

（1）求实数m的取值范围；

（2）在直线l:y=x+2上存在一点E，使得?|EF₁|+|EF₂|取得最小值，求此最小值及此时椭圆的方程；

（3）在条件（2）下的椭圆方程，是否存在斜率为k（k≠0）的直线l与椭圆交于不同的两点A、B，满足=，且使得过点N（0，-1）、Q的直线，有·=0？若存在，求出k的取值范围，若不存在，说明理由.

Answer 1

解析：（1）∵|MF₁|+|MF₂|=2,|MF₁|²+|MF₂|²=4m,

而|MF₁|²+|MF₂|²≥，

∴4m≥2(m+1),解得m≥1.

（2）由

得(m+2)x²+4(m+1)x+3(m+1)=0.

Δ=16(m+1)²-12(m+2)(m+1)=4(m+1)(m-2)≥0.

解得m≥2或m≤-1（舍去），∴m≥2.

此时|EF₁|+|EF₂|=2m+1≥2,

当且仅当m=2时|EF₁|+|EF₂|取得最小值2，此时椭圆方程为+y²=1.

（3）设两点AB的坐标分别为A（x₁,y₁）、B（x₂,y₂），中点Q（x,y），

则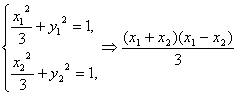+(y₁+y₂)(y₁-y₂)=0,

∴AB中点Q的轨迹为直线

y=-x                                                                                                          ①

在椭圆内的部分.

又由·=0，得过点N（0，-1），且斜率为-的直线方程为y=-x-1,          ②

由①②可得点Q的坐标为（,）,

∵点Q必在椭圆内，

∴＜1.解得k²＜1,

又k≠0,∴k∈(-1,0)∪(0,1).