
 .
. 对所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数m的取值范围.
对所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数m的取值范围.
 的图象上存在两个不同的点
的图象上存在两个不同的点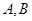 ,使直线
,使直线 恰好与
恰好与 轴垂直,设
轴垂直,设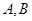 的横坐标为
的横坐标为 ,且
,且 ,然后证得
,然后证得 ;推出函数
;推出函数 在
在 上是增函数,这与这与
上是增函数,这与这与 假设矛盾,可得假设不成立,命题得证.
假设矛盾,可得假设不成立,命题得证. 的最大值小于或等于
的最大值小于或等于 ,结合(1)的过程,可求出其最大值
,结合(1)的过程,可求出其最大值 ,即整理的:
,即整理的: .令关于
.令关于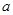 的一次函数
的一次函数 g(a)=m2+2am,则有
g(a)=m2+2am,则有 ,由此求得m的范围.
,由此求得m的范围.| 试题解析:解:(1)假设函数f(x)的图象上存在两个不同的点A,B,使直线AB恰好与y轴垂直, 则A、B两点的纵坐标相同,设它们的横坐标分别为 x1和x2,且x1<x2. 则f(x1)﹣f(x2)=f(x1)+f(﹣x2)=  [x1+(﹣x2)]. [x1+(﹣x2)].由于  >0,且[x1+(﹣x2)]<0,∴f(x1)﹣f(x2)<0, >0,且[x1+(﹣x2)]<0,∴f(x1)﹣f(x2)<0,故函数f(x)在[﹣1,1]上是增函数. 这与假设矛盾,故假设不成立,即 函数f(x)的图象上不存在两个不同的点A,B,使直线AB恰好与y轴垂直. (2)由于  对所有x∈[﹣1,1],a∈[﹣1,1]恒成立, 对所有x∈[﹣1,1],a∈[﹣1,1]恒成立,∴故函数f(x)的最大值小于或等于2(m2+2am+1). 由于由(1)可得,函数f(x)是[﹣1,1]的增函数,故函数f(x)的最大值为f(1)=2, ∴2(m2+2am+1)≥2,即 m2+2am≥0. 令关于a的一次函数g(a)=m2+2am,则有  , ,解得 m≤﹣2,或m≥2,或 m=0,故所求的m的范围是{m|m≤﹣2,或m≥2,或 m=0}. |


科目:高中数学 来源:不详 题型:解答题
 为圆心的两个同心圆弧
为圆心的两个同心圆弧 、弧
、弧 以及两条线段
以及两条线段 和
和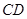 围成的封闭图形.花坛设计周长为30米,其中大圆弧
围成的封闭图形.花坛设计周长为30米,其中大圆弧 所在圆的半径为10米.设小圆弧
所在圆的半径为10米.设小圆弧 所在圆的半径为
所在圆的半径为 米(
米( ),圆心角为
),圆心角为 弧度.
弧度.
 关于
关于 的函数关系式;
的函数关系式; ,当
,当 为何值时,
为何值时, 取得最大值?
取得最大值?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (单位:元,
(单位:元, )的平方成正比.
)的平方成正比. 的函数;
的函数;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.y=x2 | B.y=x+1 | C.y=2x | D.y=log2|x| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com