
【题目】如图,在四棱锥![]() 中,
中,![]() ,底面
,底面![]() 为边长为
为边长为![]() 的菱形,且
的菱形,且![]() .
.
(1)证明:![]() ;
;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD-A1B1C1D1中,AD//平面BCC1B1,AD⊥DB.求证:

(1)BC//平面ADD1A1;
(2)平面BCC1B1⊥平面BDD1B1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型企业生产的某批产品细分为![]() 个等级,为了了解这批产品的等级分布情况,从仓库存放的
个等级,为了了解这批产品的等级分布情况,从仓库存放的![]() 件产品中随机抽取
件产品中随机抽取![]() 件进行检测、分类和统计,并依据以下规则对产品进行打分:
件进行检测、分类和统计,并依据以下规则对产品进行打分:![]() 级或
级或![]() 级产品打
级产品打![]() 分;
分;![]() 级或
级或![]() 级产品打
级产品打![]() 分;
分;![]() 级、
级、![]() 级、
级、![]() 级或
级或![]() 级产品打
级产品打![]() 分;其余产品打
分;其余产品打![]() 分.现在有如下检测统计表:
分.现在有如下检测统计表:
等级 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
频数 | 10 | 90 | 100 | 200 | 200 | 100 | 100 | 100 | 70 | 30 |
规定:打分不低于![]() 分的为优良级.
分的为优良级.
(1)①试估计该企业库存的![]() 件产品为优良级的概率;
件产品为优良级的概率;
②请估计该企业库存的![]() 件产品的平均得分.
件产品的平均得分.
(2)从该企业库存的![]() 件产品中随机抽取
件产品中随机抽取![]() 件,请估计这
件,请估计这![]() 件产品的打分之和为
件产品的打分之和为![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某工厂生产的某种产品中抽取1000件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
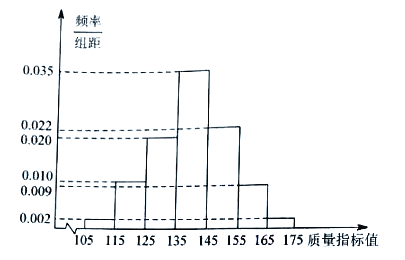
(1)求这1000件产品质量指标值的样本平均数![]() 和样本方差
和样本方差![]() (同一组数据用该区间的中点值作代表)
(同一组数据用该区间的中点值作代表)
(2)由频率分布直方图可以认为,这种产品的质量指标值![]() 服从正态分布
服从正态分布![]() ,其中以
,其中以![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(ⅰ)利用该正态分布,求![]() ;
;
(ⅱ)某用户从该工厂购买了100件这种产品,记![]() 表示这100件产品中质量指标值为于区间(127.6,140)的产品件数,利用(ⅰ)的结果,求
表示这100件产品中质量指标值为于区间(127.6,140)的产品件数,利用(ⅰ)的结果,求![]() .
.
附:![]() .若
.若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准:用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了100位居民某年的月均用水量(单位:吨),制作了频率分布直方图,
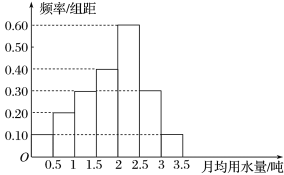
(Ⅰ)用该样本估计总体:
(1)估计该市居民月均用水量的平均数;
(2)如果希望86%的居民每月的用水量不超出标准,则月均用水量a的最低标准定为多少吨?
(Ⅱ)若将频率视为概率,现从该市某大型生活社区随机调查3位居民的月均用水量,其中月均用水量不超过2.5吨的人数为X,求X的分布列和均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值;
上的最大值;
(2)令![]() ,若
,若![]() 在区间
在区间![]() 上为单调递增函数,求
上为单调递增函数,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,函数
时,函数![]() 的图象与
的图象与![]() 轴交于两点
轴交于两点![]() ,且
,且![]() ,又
,又![]() 是
是![]() 的导函数.若正常数
的导函数.若正常数![]() 满足条件
满足条件![]() .证明:
.证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大学生赵敏利用寒假参加社会实践,对机械销售公司7月份至12月份销售某种机械配件的销售量及销售单价进行了调查,销售单价![]() 和销售量
和销售量![]() 之间的一组数据如下表所示:
之间的一组数据如下表所示:
月份 | 7 | 8 | 9 | 10 | 11 | 12 |
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
销售量 | 11 | 10 | 8 | 6 | 5 | 14 |
(1)根据7至11月份的数据,求出![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元,则认为所得到的回归直线方程是理想的,试问(1)中所得到的回归直线方程是否理想?
(3)预计在今后的销售中,销售量与销售单价仍然服从(1)中的关系,若该种机器配件的成本是2.5元/件,那么该配件的销售单价应定为多少元才能获得最大利润?(注:利润=销售收入-成本).
参考公式:回归直线方程![]() ,其中
,其中 ,参考数据:
,参考数据: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com