
【题目】已知函数f(x)= ![]() x2﹣(2a+2)x+(2a+1)lnx
x2﹣(2a+2)x+(2a+1)lnx
(1)若曲线y=f(x)在点(2,f(2))处的切线的斜率小于0,求f(x)的单调区间;
(2)对任意的a∈[ ![]() ,
, ![]() ],x1 , x2∈[1,2](x1≠x2),恒有|f(x1)﹣f(x2)|<λ|
],x1 , x2∈[1,2](x1≠x2),恒有|f(x1)﹣f(x2)|<λ| ![]() ﹣
﹣ ![]() |,求正数λ的取值范围.
|,求正数λ的取值范围.
【答案】
(1)解:函数f(x)= ![]() x2﹣(2a+2)x+(2a+1)lnx的导数
x2﹣(2a+2)x+(2a+1)lnx的导数
f′(x)=x﹣(2a+2)+ ![]() =
= ![]() ,x>0,
,x>0,
由题意可得f′(2)= ![]() <0,可得a>
<0,可得a> ![]() ,2a+1>2>1,
,2a+1>2>1,
由f′(x)>0,可得x>2a+1或0<x<1;f′(x)<0,可得1<x<2a+1.
即有f(x)的增区间为(0,1),(2a+1,+∞);减区间为(1,2a+1);
(2)解:由a∈[ ![]() ,
, ![]() ],可得2a+1∈[4,6],
],可得2a+1∈[4,6],
由(1)可得f(x)在[1,2]递减.
设1≤x1<x2≤2,即有f(x1)>f(x2), ![]() >
> ![]() ,
,
原不等式即为f(x1)﹣λ ![]() <f(x2)﹣λ
<f(x2)﹣λ ![]()
对任意的a∈[ ![]() ,
, ![]() ],x1,x2∈[1,2]恒成立,
],x1,x2∈[1,2]恒成立,
令g(x)=f(x)﹣ ![]() ,即有g(x1)<g(x2),即为g(x)在[1,2]递增,
,即有g(x1)<g(x2),即为g(x)在[1,2]递增,
即有g′(x)≥0对任意的a∈[ ![]() ,
, ![]() ],x1,x2∈[1,2]恒成立,
],x1,x2∈[1,2]恒成立,
即x﹣(2a+2)+ ![]() +
+ ![]() ≥0,即为x3﹣(2a+2)x2+(2a+1)x+λ≥0,
≥0,即为x3﹣(2a+2)x2+(2a+1)x+λ≥0,
则(2x﹣2x2)a+x3﹣2x2+x+λ≥0,a∈[ ![]() ,
, ![]() ],
],
由x∈[1,2],可得2x﹣2x2≤0,只需 ![]() (2x﹣2x2)a+x3﹣2x2+x+λ≥0.
(2x﹣2x2)a+x3﹣2x2+x+λ≥0.
即x3﹣7x2+6x+λ≥0对x∈[1,2]恒成立,
令h(x)=x3﹣7x2+6x+λ,h′(x)=3x2﹣14x+6≤0在1≤x≤2恒成立,
则有h(x)在[1,2]递减,可得h(2)取得最小值,且为﹣8+λ≥0,
解得λ≥8.即有正数λ的取值范围是[8,+∞).
【解析】(1)求出函数的导数,并分解因式,由题意可得f′(2)= <0,再由导数大于0,可得增区间,导数小于0,可得减区间,注意定义域;(2)求出2a+1的范围,可得f(x)在[1,2]递减,由题意可得原不等式即为f(x1)﹣λ
![]() <f(x2)﹣λ
<f(x2)﹣λ ![]()
对任意的a∈[ ![]() ,
, ![]() ],x1 , x2∈[1,2]恒成立,令g(x)=f(x)﹣
],x1 , x2∈[1,2]恒成立,令g(x)=f(x)﹣ ![]() ,即有g(x1)<g(x2),即为g(x)在[1,2]递增,求出g(x)的导数,令导数大于等于0,再由一次函数的单调性可得只需
,即有g(x1)<g(x2),即为g(x)在[1,2]递增,求出g(x)的导数,令导数大于等于0,再由一次函数的单调性可得只需 ![]() (2x﹣2x2)a+x3﹣2x2+x+λ≥0.即x3﹣7x2+6x+λ≥0对x∈[1,2]恒成立,令h(x)=x3﹣7x2+6x+λ,求出导数,求得单调区间和最小值,解不等式即可得到所求范围.
(2x﹣2x2)a+x3﹣2x2+x+λ≥0.即x3﹣7x2+6x+λ≥0对x∈[1,2]恒成立,令h(x)=x3﹣7x2+6x+λ,求出导数,求得单调区间和最小值,解不等式即可得到所求范围.
【考点精析】掌握利用导数研究函数的单调性是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
【题目】在“新零售”模式的背景下,某大型零售公司为推广线下分店,计划在S市的A区开设分店.为了确定在该区开设分店的个数,该公司对该市已开设分店的其他区的数据作了初步处理后得到下列表格.记x表示在各区开设分店的个数,y表示这x个分店的年收入之和.
x(个) | 2 | 3 | 4 | 5 | 6 |
y(百万元) | 2.5 | 3 | 4 | 4.5 | 6 |
(1)在年收入之和为2.5(百万元)和3(百万元)两区中抽取两分店调查,求这两分店来自同一区的概率
(2)该公司已经过初步判断,可用线性回归模型拟合y与x的关系,求y关于x的线性回归方程;
(3)假设该公司在A区获得的总年利润z(单位:百万元)与x,y之间的关系为z=y-0.05x2-1.4,请结合(1)中的线性回归方程,估算该公司应在A区开设多少个分店,才能使A区平均每个分店的年利润最大?
参考公式:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,且函数g(x)=loga(x2+x+2)(a>0,且a≠1)在[﹣
,且函数g(x)=loga(x2+x+2)(a>0,且a≠1)在[﹣ ![]() ,1]上的最大值为2,若对任意x1∈[﹣1,2],存在x2∈[0,3],使得f(x1)≥g(x2),则实数m的取值范围是( )
,1]上的最大值为2,若对任意x1∈[﹣1,2],存在x2∈[0,3],使得f(x1)≥g(x2),则实数m的取值范围是( )
A.(﹣∞,﹣ ![]() ]
]
B.(﹣∞, ![]() ]
]
C.[ ![]() ,+∞)
,+∞)
D.[﹣ ![]() ,+∞]
,+∞]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,我国PM2.5标准采用世界卫生组织设定的最宽限值,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米及其以上空气质量为超标.
某试点城市环保局从该市市区2016年全年每天的PM2.5监测数据中随机抽取6天的数据作为样本,监测值茎叶图(十位为茎,个位为叶)如图所示,若从这6天的数据中随机抽出2天,

(1)求恰有一天空气质量超标的概率;
(2)求至多有一天空气质量超标的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将红、黑、蓝、白5张纸牌(其中白纸牌有2张)随机分发给甲、乙、丙、丁4个人,每人至少分得1张,则下列两个事件为互斥事件的是( )
A. 事件“甲分得1张白牌”与事件“乙分得1张红牌”
B. 事件“甲分得1张红牌”与事件“乙分得1张蓝牌”
C. 事件“甲分得1张白牌”与事件“乙分得2张白牌”
D. 事件“甲分得2张白牌”与事件“乙分得1张黑牌”
查看答案和解析>>
科目:高中数学 来源: 题型:
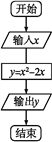
【题目】求函数y=![]() 的值的程序框图如图所示.
的值的程序框图如图所示.
(1)指出程序框图中的错误,并写出算法;
(2)重新绘制解决该问题的程序框图,并回答下面提出的问题.
①要使输出的值为正数,输入的x的值应满足什么条件?
②要使输出的值为8,输入的x值应是多少?
③要使输出的y值最小,输入的x值应是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥![]() ,侧面
,侧面![]() 是边长为2的正三角形,且平面
是边长为2的正三角形,且平面![]() 平面
平面![]() ,底面
,底面![]() 是菱形,且
是菱形,且![]() ,
, ![]() 为棱
为棱![]() 上的动点,且
上的动点,且![]() .
.

(1)求证: ![]() ;
;
(2)试确定![]() 的值,使得二面角
的值,使得二面角![]() 的余弦值为
的余弦值为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数y=f(x)满足f(﹣x)+f(x)=0且f(x+1)=f(x﹣1),若x∈(0,1)时,f(x)=log2 ![]() ,则y=f(x)在(1,2)内是( )
,则y=f(x)在(1,2)内是( )
A.单调增函数,且f(x)<0
B.单调减函数,且f(x)<0
C.单调增函数,且f(x)>0
D.单调增函数,且f(x)>0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com