
【题目】如图所示,在正方体ABCD-A′B′C′D′中: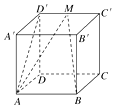
(1)求二面角D′-AB-D的大小;
(2)若M是C′D′的中点,求二面角M-AB-D的大小.
【答案】
(1)解:在正方体ABCD-A′B′C′D′中,AB⊥平面ADD′A′,所以AB⊥AD′,AB⊥AD,因此∠D′AD为二面角D′-AB-D的平面角,在Rt△D′DA中,∠D′AD=45°,所以二面角D′-AB-D的大小为45°
(2)解:因为M是C′D′的中点,所以MA=MB,取AB的中点N,连接MN,则MN⊥AB.取CD的中点H,连接HN,则HN⊥AB.
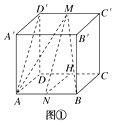
从而∠MNH是二面角M-AB-D的平面角.∠MNH=45°,所以二面角M-AB-D的大小为45°.
【解析】(1)利用正方体的性质结合已知条件可得出线面垂直进而找到二面角D′-AB-D的平面角,再利用解三角形的知识求出平面角的大小进而得出二面角的大小。(2)由已知条件作出辅助线借助正方体的性质可找到∠MNH是二面角M-AB-D的平面角,根据已知条件即可求出平面角的大小故可得二面角的大小。
【考点精析】根据题目的已知条件,利用直线与平面垂直的性质的相关知识可以得到问题的答案,需要掌握垂直于同一个平面的两条直线平行.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某大学中文系共有本科生5000人,其中一、二、三、四年级的学生比为5:4:3:1,要用分层抽样的方法从该系所有本科生中抽取一个容量为260的样本,则应抽二年级的学生( )
A.100人
B.60人
C.80人
D.20人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各对直线不互相垂直的是( )
A.l1的倾斜角为120°,l2过点P(1,0),Q(4, ![]() )
)
B.l1的斜率为- ![]() ,l2过点P(1,1),Q
,l2过点P(1,1),Q ![]()
C.l1的倾斜角为30°,l2过点P(3, ![]() ),Q(4,2
),Q(4,2 ![]() )
)
D.l1过点M(1,0),N(4,-5),l2过点P(-6,0),Q(-1,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若抛物线的顶点是双曲线x2﹣y2=1的中心,焦点是双曲线的右顶点
(1)求抛物线的标准方程;
(2)若直线l过点C(2,1)交抛物线于M,N两点,是否存在直线l,使得C恰为弦MN的中点?若存在,求出直线l方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)求函数f(x)的单调区间;
(2)若g(x)=xf(x)+mx在区间(0,e]上的最大值为﹣3,求m的值;
(3)若x≥1时,有不等式f(x)≥ ![]() 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位决定建造一批简易房(房型为长方体状,房高2.5米),前后墙用2.5米高的彩色钢板,两侧用2.5米高的复合钢板,两种钢板的价格都用长度来计算(即:钢板的高均为2.5米,用钢板的长度乘以单价就是这块钢板的价格),每米单价:彩色钢板为450元,复合钢板为200元.房顶用其它材料建造,每平方米材料费为200元.每套房材料费控制在32000元以内.
(1)设房前面墙的长为x,两侧墙的长为y,所用材料费为p,试用x,y表示p;
(2)在材料费的控制下简易房面积S的最大值是多少?并指出前面墙的长度x应为多少米时S最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人. (Ⅰ)求该专业毕业总人数N和90~95分数段内的人数n;
(Ⅱ)现欲将90~95分数段内的n名人分配到几所学校,从中安排2人到甲学校去,若n人中仅有两名男生,求安排结果至少有一名男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=lnx+ ![]() x2 .
x2 .
(1)求曲线f(x)在x=1处的切线方程;
(2)设P为曲线f(x)上的点,求曲线C在点P处切线的斜率的最小值及倾斜角α的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com