
 如图,BD=CE,G、H为BC、DE中点,AB=AC,FD=FE,∠BAC=∠DFE.求证:AF∥GH.
如图,BD=CE,G、H为BC、DE中点,AB=AC,FD=FE,∠BAC=∠DFE.求证:AF∥GH. 分析 如图,AI∥BD,DI∥BA,AK∥CE,KE∥AC,M为BE中点,证明△IDF≌△KEF,故△AIF≌△AKF,所以∠IAF=∠KAF=$\frac{1}{2}$(180-∠B-∠D),而∠MGH=$\frac{1}{2}$(180-∠GMH)=$\frac{1}{2}$(180-∠B-∠D)=∠KAF,所以MG∥EC∥KA即可证明结论.
解答 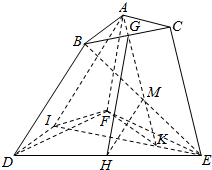 证明:如图,AI∥BD,DI∥BA,AK∥CE,KE∥AC,M为BE中点,
证明:如图,AI∥BD,DI∥BA,AK∥CE,KE∥AC,M为BE中点,
因为∠BAC=∠DFE,
所以∠IDF=ID与DF夹角=AB与DF夹角=BC与DE夹角,∠ACB=∠FED,
所以∠FEK=FE与EK夹角=FE与AC夹角=DE与BC夹角.
因此∠IDF=∠FEK.
而ID=BA=CA=KE,DF=EF,
故△IDF≌△KEF,
故△AIF≌△AKF,
所以∠IAF=∠KAF=$\frac{1}{2}$(180-∠B-∠D),
而∠MGH=$\frac{1}{2}$(180-∠GMH)=$\frac{1}{2}$(180-∠B-∠D)=∠KAF,
所以MG∥EC∥KA,
因此GH∥AF.
点评 本题考查两条直线的平行,考查学生分析解决问题的能力,有难度.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=x|x-1|.
已知函数f(x)=x|x-1|.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PA上的一点.
在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PA上的一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | -$\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com