
有6名男医生,4名女医生.
(1)选3名男医生,2名女医生,让这5名医生到5个不同地区去巡回医疗,共有多少种不同方法?
(2)把10名医生分成两组,每组5人且每组都要有女医生,则有多少种不同分法?若将这两组医生分派到两地去,并且每组选出正副组长两人,又有多少种不同方案?
(1)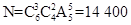 ; (2)
; (2) 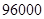
解析试题分析:(1)本题中不仅要选出5名医生(元素),还要求分配到5个地区(空位),因此是一道“既选又排”的排列组合综合问题,解决这类问题的方法是“先选后排”,同时要注意特殊元素、特殊位置优先安排的原则。
(2)首先将分成以下两类情况第一类:一组中女医生1人,男医生4人,另一组中女医生3人,男医生2人;第二类:两组中人数都有女医生2人男医生3人;最后将这两组医生分派到两地去,并且每组选出正副组长两人,是排列问题.
(1)分三步完成.
第一步:从6名男医生中选3名有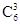 种方法;
种方法;
第二步:从4名女医生中选2名有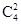 种方法;
种方法;
第三步:对选出的5人分配到5个地区有A种方法.
根据分步乘法计数原理,共有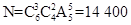 (种).
(种).
(2)医生的选法有以下两类情况:
第一类:一组中女医生1人,男医生4人,另一组中女医生3人,男医生2人.共有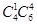 种不同的分法;
种不同的分法;
第二类:两组中人数都有女医生2人男医生3人.因为组与组之间无顺序,故共有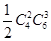 种不同的分法.
种不同的分法.
因此,把10名医生分成两组,每组5人且每组都要有女医生的不同的分法共有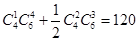 种.
种.
若将这两组医生分派到两地去,并且每组选出正副组长两人,则共有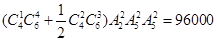 种不同方案
种不同方案
考点:排列组合,计数原理


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
有3名男生,4名女生,在下列不同要求下,求不同的排列方法总数:
(1)选其中5人排成一排;
(2)排成前后两排,前排3人,后排4人;
(3)全体排成一排,甲不站在排头也不站在排尾;
(4)全体排成一排,女生必须站在一起;
(5)全体排成一排,男生互不相邻;
(6)全体排成一排,甲、乙两人中间恰好有3人.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
由数字1、2、3、4、5、6组成无重复数字的数中,求:
(1)六位偶数的个数;
(2)求三个偶数互不相邻的六位数的个数;
(3)求恰有两个偶数相邻的六位数的个数;
(4)奇数字从左到右,从小到大依次排列的六位数的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2013•浙江)设袋子中装有a个红球,b个黄球,c个蓝球,且规定:取出一个红球得1分,取出一个黄球2分,取出蓝球得3分.
(1)当a=3,b=2,c=1时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量ξ为取出此2球所得分数之和.,求ξ分布列;
(2)从该袋子中任取(且每球取到的机会均等)1个球,记随机变量η为取出此球所得分数.若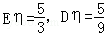 ,求a:b:c.
,求a:b:c.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某体育彩票规定:从01到36共36个号中抽出7个号为一注,每注2元.某人想先选定吉利号18,然后从01至17中选3个连续的号,从19至29中选2个连续的号,从30至36中选1个号组成一注.若这个人要把这种要求的号全买下,则至少要花多少元钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com