
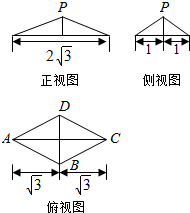
 已知四棱锥P-ABCD的三视图如图所示,其中俯视图是菱形,正视图和侧视图都是等腰三角形,已知M为BC上一点,且BM=$\frac{1}{2}$,PA⊥PM.
已知四棱锥P-ABCD的三视图如图所示,其中俯视图是菱形,正视图和侧视图都是等腰三角形,已知M为BC上一点,且BM=$\frac{1}{2}$,PA⊥PM.分析 (1)画出几何体的直观图,结合已知三视图可得OA=OC=$\sqrt{3}$,OB=OD=1,BM=$\frac{1}{2}$,∠OBC=∠OBA=60°,结合余弦定理和勾股定理,可求出四棱锥P-ABCD的高;
(2)三棱锥M-PAD,即棱锥P-ADM的体积等于棱锥P-ABCD的体积的$\frac{1}{2}$,若四棱锥M-AEFD与P-ABCD的体积之比为$\frac{1}{3}$,则四棱锥M-AEFD与M-PAD的体积之比为$\frac{2}{3}$,进而得到答案.
解答 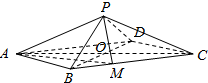 解:(1)四棱锥P-ABCD的直观图如下图所示:
解:(1)四棱锥P-ABCD的直观图如下图所示:
由三视图可得:OA=OC=$\sqrt{3}$,OB=OD=1,BM=$\frac{1}{2}$,
则∠OBC=∠OBA=60°,
设四棱锥P-ABCD的高PO=a,
则AM=$\sqrt{{AB}^{2}+{BM}^{2}-2AB•BM•cos∠ABM}$=$\sqrt{4+\frac{1}{4}+1}$=$\frac{\sqrt{21}}{2}$,
PA=$\sqrt{{PO}^{2}+{OA}^{2}}$=$\sqrt{{a}^{2}+3}$,
OM=$\sqrt{{OB}^{2}+{BM}^{2}-2OB•BM•cos∠OBM}$=$\sqrt{1+\frac{1}{4}-\frac{1}{2}}$=$\frac{\sqrt{3}}{2}$,
PM=$\sqrt{{PO}^{2}+{OM}^{2}}$=$\sqrt{{a}^{2}+\frac{3}{4}}$,
∵PA⊥PM,
∴PA2+PM2=AM2,即$2{a}^{2}+3\frac{3}{4}=\frac{21}{4}$,
解得:a=$\frac{\sqrt{3}}{2}$,
即四棱锥P-ABCD的高为$\frac{\sqrt{3}}{2}$,
(2)三棱锥M-PAD,即棱锥P-ADM的体积等于棱锥P-ABCD的体积的$\frac{1}{2}$,
四棱锥M-AEFD与三棱锥M-PAD同高,
若四棱锥M-AEFD与P-ABCD的体积之比为$\frac{1}{3}$,
则四棱锥M-AEFD与M-PAD的体积之比为$\frac{2}{3}$,
即梯形AEFD的面积是△PAD面积的$\frac{2}{3}$,
则△PEF的面积是△PAD面积的$\frac{1}{3}$
又由$\frac{PE}{PA}$=$\frac{PF}{PD}$=λ,
故${λ}^{2}=\frac{1}{3}$,
解得:$λ=\frac{\sqrt{3}}{3}$
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
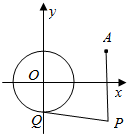 如图,已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P向圆O引切线PQ,切点为Q,且有|PQ|=|PA|.
如图,已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P向圆O引切线PQ,切点为Q,且有|PQ|=|PA|.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com