
【题目】某市《城市总体规划(![]() 年)》提出到2035年实现“15分钟社区生活圈”全覆盖的目标,从教育与文化、医疗与养老、交通与购物、休闲与健身4个方面构建“15分钟社区生活圈“指标体系,并依据“15分钟社区生活圈”指数高低将小区划分为:优质小区(指数为
年)》提出到2035年实现“15分钟社区生活圈”全覆盖的目标,从教育与文化、医疗与养老、交通与购物、休闲与健身4个方面构建“15分钟社区生活圈“指标体系,并依据“15分钟社区生活圈”指数高低将小区划分为:优质小区(指数为![]() 、良好小区(指数为0.4-0.63、中等小区(指数为0.2~0.4)以及待改进小区(指数为0-0.2)4个等级.下面是三个小区4个方面指标值的调查数据:
、良好小区(指数为0.4-0.63、中等小区(指数为0.2~0.4)以及待改进小区(指数为0-0.2)4个等级.下面是三个小区4个方面指标值的调查数据:
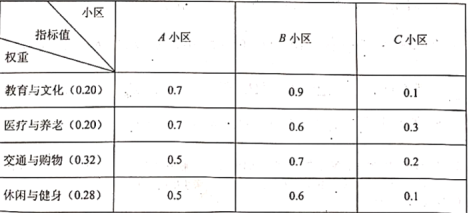
注:每个小区”15分钟社区生活圈”指数![]() 其中
其中![]() 、
、![]() 、
、![]() 、
、![]() 为该小区四个方面的权重,
为该小区四个方面的权重,![]() 为该小区四个方面的指标值(小区每一个方面的指标值为
为该小区四个方面的指标值(小区每一个方面的指标值为![]() 之间的一个数值)
之间的一个数值)
现有100个小区的“15分钟社区生活圈“指数数据,整理得到如下频数分布表:

(1)分别判断A、B、C三个小区是否是优质小区,并说明理由;
(2)对这100个小区按照优质小区、良好小区、中等小区和待改进小区进行分层抽样,抽取10个小区进行调查,若在抽取的10个小区中再随机地选取2个小区做深入调查,记这2个小区中为优质小区的个数为ζ,求ζ的分布列及数学期望.
【答案】(1)![]() 小区不是优质小区;
小区不是优质小区;![]() 小区是优质小区;
小区是优质小区; ![]() 小区不是优质小区;见解析(2)见解析
小区不是优质小区;见解析(2)见解析
【解析】
(1)分别求出![]() 、
、![]() 、
、![]() 三个小区指数,由此能判断
三个小区指数,由此能判断![]() ,
,![]() ,
,![]() 三个小区是否是优质小区.
三个小区是否是优质小区.
(2)对这100个小区按照优质小区、良好小区、中等小区和待改进小区进行分层抽样,抽取10个小区进行调查,抽到优质小区的个数为4个,抽到良好小区的个数为3个,抽到中等小区的个数为2个,抽到待改进小区的个数为1个,在抽取的10个小区中再随机地选取2个小区做深入调查,记这2个小区中为优质小区的个数为![]() ,则
,则![]() 的可能取值为0,1,2,分别求出相应的概率,由此能求出
的可能取值为0,1,2,分别求出相应的概率,由此能求出![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
解:(1)![]() 小区的指数
小区的指数![]() ,
,
![]() ,所以
,所以![]() 小区不是优质小区;
小区不是优质小区;
![]() 小区的指数
小区的指数![]() ,
,
![]() ,所以
,所以![]() 小区是优质小区;
小区是优质小区;
![]() 小区的指数
小区的指数![]() ,
,
![]() ,所以
,所以![]() 小区不是优质小区;
小区不是优质小区;
(2)依题意,抽取![]() 个小区中,共有优质小区
个小区中,共有优质小区![]() 个,
个,
其它小区![]() 个
个
依题意![]() 的所有可能取值为
的所有可能取值为![]() 、
、![]() 、
、![]() .
.
![]() ,
,![]() ,
,
![]() .
.
则![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 |
|
|
|
|
![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点为
的左、右焦点为![]() ,
,![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() 面积的最大值为
面积的最大值为![]() ,周长为6.
,周长为6.
(1)求椭圆![]() 的方程,并求椭圆
的方程,并求椭圆![]() 的离心率;
的离心率;
(2)已知直线![]() :
:![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,若在
,若在![]() 轴上存在点
轴上存在点![]() ,使得
,使得![]() 与
与![]() 中点的连线与直线
中点的连线与直线![]() 垂直,求实数
垂直,求实数![]() 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,其右顶点为
,其右顶点为![]() ,下顶点为
,下顶点为![]() ,定点
,定点![]() ,
,![]() 的面积为
的面积为![]() ,过点
,过点![]() 作与
作与![]() 轴不重合的直线
轴不重合的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,直线
两点,直线![]() 分别与
分别与![]() 轴交于
轴交于![]() 两点.
两点.
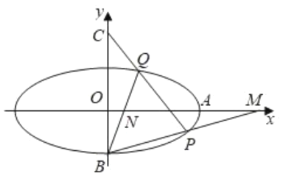
(1)求椭圆![]() 的方程;
的方程;
(2)试探究![]() 的横坐标的乘积是否为定值,若是,请求出该定值;若不是,请说明理由.
的横坐标的乘积是否为定值,若是,请求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,平面![]() 平面
平面![]() ,且四边形
,且四边形![]() 为矩形,四边形
为矩形,四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() .
.
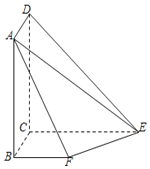
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成锐二面角的大小;
所成锐二面角的大小;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,由直三棱柱![]() 和四棱锥
和四棱锥![]() 构成的几何体中,
构成的几何体中, ![]() ,平面
,平面![]() 平面
平面![]() .
.
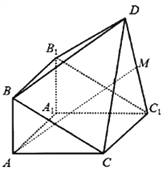
(Ⅰ)求证: ![]() ;
;
(Ⅱ)在线段![]() 上是否存在点
上是否存在点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?若存在,求
?若存在,求![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水果批发商经销某种水果(以下简称A水果),购入价为300元/袋,并以360元/袋的价格售出,若前8小时内所购进的A水果没有售完,则批发商将没售完的A水果以220元/袋的价格低价处理完毕(根据经验,2小时内完全能够把A水果低价处理完,且当天不再购进).该水果批发商根据往年的销量,统计了100天A水果在每天的前8小时内的销售量,制成如下频数分布条形图.
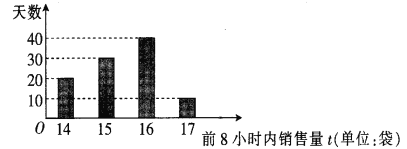
现以记录的100天的A水果在每天的前8小时内的销售量的频率作为A水果在一天的前8小时内的销售量的概率,记X表示A水果一天前8小时内的销售量,n表示水果批发商一天批发A水果的袋数.
(1)求X的分布列;
(2)以日利润的期望值为决策依据,在![]() 与
与![]() 中选其一,应选用哪个?
中选其一,应选用哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年10月,工信部颁发了国内首个![]() 无线电通信设备进网许可证,标志着
无线电通信设备进网许可证,标志着![]() 基站设备将正式接入公用电信商用网络.某
基站设备将正式接入公用电信商用网络.某![]() 手机生产商拟升级设备生产
手机生产商拟升级设备生产![]() 手机,有两种方案可供选择,方案1:直接引进
手机,有两种方案可供选择,方案1:直接引进![]() 手机生产设备;方案2:对已有的
手机生产设备;方案2:对已有的![]() 手机生产设备进行技术改造,升级到
手机生产设备进行技术改造,升级到![]() 手机生产设备.该生产商对未来
手机生产设备.该生产商对未来![]() 手机销售市场行情及回报率进行大数据模拟,得到如下统计表:
手机销售市场行情及回报率进行大数据模拟,得到如下统计表:
市场销售状态 | 畅销 | 平销 | 滞销 | |
市场销售状态概率 |
|
|
| |
预期年利润数值(单位:亿元) | 方案1 | 70 | 40 | -40 |
方案2 | 60 | 30 | -10 | |
(1)以预期年利润的期望值为依据,求![]() 的取值范围,讨论该生产商应该选择哪种方案进行设备升级?
的取值范围,讨论该生产商应该选择哪种方案进行设备升级?
(2)设该生产商升级设备后生产的![]()
![]() 万部,通过大数据模拟核算,选择方案1所生产的
万部,通过大数据模拟核算,选择方案1所生产的![]() 手机年度总成本
手机年度总成本![]() (亿元),选择方案2所生产的
(亿元),选择方案2所生产的![]() 手机年度总成为
手机年度总成为![]() (亿元).已知
(亿元).已知![]() ,当所生产的
,当所生产的![]() 手机市场行情为畅销、平销和滞销时,每部手机销售单价分别为0.8万元,
手机市场行情为畅销、平销和滞销时,每部手机销售单价分别为0.8万元,![]() (万元),
(万元),![]() (万元),根据(1)的决策,求该生产商所生产的
(万元),根据(1)的决策,求该生产商所生产的![]() 手机年利润期望的最大值?并判断这个年利润期望的最大值能否达到预期年利润数值.
手机年利润期望的最大值?并判断这个年利润期望的最大值能否达到预期年利润数值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥P﹣ABC中.AB⊥BC,△PAC为等边三角形,二面角P﹣AC﹣B的余弦值为![]() ,当三棱锥的体积最大时,其外接球的表面积为8π.则三棱锥体积的最大值为( )
,当三棱锥的体积最大时,其外接球的表面积为8π.则三棱锥体积的最大值为( )
A.1B.2C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com