
【题目】下列方程中,没有实数根的是( )
A.2x+3=0
B.![]() ﹣1=0
﹣1=0
C.![]()
D.![]() +x+1=0
+x+1=0
【答案】D
【解析】解:A、2x+3=0,解得:x=﹣ ![]() ,
,
∴A中方程有一个实数根;
B、在x2﹣1=0中,
△=02﹣4×1×(﹣1)=4>0,
∴B中方程有两个不相等的实数根;
C、 ![]() =1,即x+1=2,
=1,即x+1=2,
解得:x=1,
经检验x=1是分式方程 ![]() =1的解,
=1的解,
∴C中方程有一个实数根;
D、在x2+x+1=0中,
△=12﹣4×1×1=﹣3<0,
∴D中方程没有实数根.
故选D.
【考点精析】关于本题考查的解一元一次方程的步骤和求根公式,需要了解先去分母再括号,移项变号要记牢.同类各项去合并,系数化“1”还没好.求得未知须检验,回代值等才算了;根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为
的棱长为![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 为线段
为线段![]() 上的动点,过点
上的动点,过点![]() ,
, ![]() ,
, ![]() 的平面截该正方体所得的截面为
的平面截该正方体所得的截面为![]() ,则下列命题正确的是__________(写出所有正确命题的编号).
,则下列命题正确的是__________(写出所有正确命题的编号).

①当![]() 时,
时, ![]() 为四边形;②当
为四边形;②当![]() 时,
时, ![]() 为等腰梯形;
为等腰梯形;
③当![]() 时,
时, ![]() 与
与![]() 的交点
的交点![]() 满足
满足![]() ;
;
④当![]() 时,
时, ![]() 为五边形;
为五边形;
⑤当![]() 时,
时, ![]() 的面积为
的面积为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
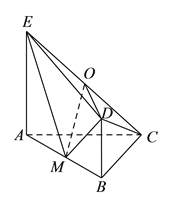
【题目】如图,平面![]() 平面
平面![]() ,
,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,四边形
,四边形![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
(I)求证:![]() 平面
平面![]() .
.
(II)求直线![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
(III)能否在![]() 上找一点
上找一点![]() ,使得
,使得![]() 平面
平面![]() ?若能,请指出点
?若能,请指出点![]() 的位置,并加以证明;若不能,请说明理由.
的位置,并加以证明;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
(1)判定AE与PD是否垂直,并说明理由.
(2)设AB=2,若H为PD上的动点,若△AHE面积的最小值为![]() , 求四棱锥P﹣ABCD的体积.
, 求四棱锥P﹣ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种药种植基地有两处种植区的药材需在下周一、周二两天内采摘完毕,基地员工一天可以完成一处种植区的采摘,由于下雨会影响药材的收益,若基地收益如下表所示:已知下周一和下周二无雨的概率相同且为![]() ,两天是否下雨互不影响,若两天都下雨的概率为
,两天是否下雨互不影响,若两天都下雨的概率为![]()

(1)求![]() 及基地的预期收益;
及基地的预期收益;
(2)若该基地额外聘请工人,可在周一当天完成全部采摘任务,若周一无雨时收益为![]() 万元,有雨时收益为
万元,有雨时收益为![]() 万元,且额外聘请工人的成本为
万元,且额外聘请工人的成本为![]() 元,问该基地是否应该额外聘请工人,请说明理由.
元,问该基地是否应该额外聘请工人,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】按照国家环保部发布的新修订的《环境空气质量标准》,规定:PM2.5的年平均浓度不得超过35微克/立方米,国家环保部门在2016年10月1日到2017年1月30日这120天对全国的PM2.5平均浓度的监测数据统计如下:
组别 | PM2.5浓度(微克/立方米) | 频数(天) |
第一组 |
| 32 |
第二组 |
| 64 |
第三组 |
| 16 |
第四组 | 115以上 | 8 |
(1)在这120天中抽取30天的数据做进一步分析,每一组应抽取多少天?
(2)在(1)中所抽取的样本PM2.5的平均浓度超过75(微克/立方米)的若干天中,随机抽取2天,求恰好有一天平均浓度超过115(微克/立方米)的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com