
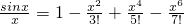 +…对x∈R且x≠0恒成立,方程
+…对x∈R且x≠0恒成立,方程 =0有无究多个根:±π,±2π,…±nπ,…,则1-
=0有无究多个根:±π,±2π,…±nπ,…,则1-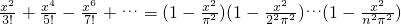 …,比较两边x2的系数可以推得1+
…,比较两边x2的系数可以推得1+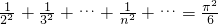 .设代数方程1-a1x2+a2x4-…+(-1)nanx2n=0有2n个不同的根:±x1,±x2,…±xn,类比上述方法可得a1=________.(用x1,x2,…,xn表示)
.设代数方程1-a1x2+a2x4-…+(-1)nanx2n=0有2n个不同的根:±x1,±x2,…±xn,类比上述方法可得a1=________.(用x1,x2,…,xn表示)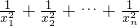 )
)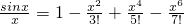 +…对x∈R且x≠0恒成立,方程
+…对x∈R且x≠0恒成立,方程 =0有无究多个根:±π,±2π,…±nπ,…,则,1-
=0有无究多个根:±π,±2π,…±nπ,…,则,1-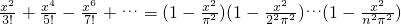 …,比较两边x2的系数可以推得1+
…,比较两边x2的系数可以推得1+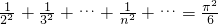 .类比推理可由代数方程1-a1x2+a2x4-…+(-1)nanx2n=0有2n个不同的根:±x1,±x2,…±xn,转化 为1-a1x2+a2x4-…+(-1)nanx2n=
.类比推理可由代数方程1-a1x2+a2x4-…+(-1)nanx2n=0有2n个不同的根:±x1,±x2,…±xn,转化 为1-a1x2+a2x4-…+(-1)nanx2n=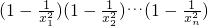 ,比较两边x2的系数即可得到答案.
,比较两边x2的系数即可得到答案.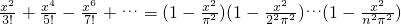 中,
中,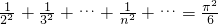 .
.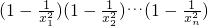 中,
中, )
) )
)

科目:高中数学 来源: 题型:
| x2 | ||
|
| x2 | ||
|
| x2 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| sinx |
| x |
| x2 |
| 3! |
| x4 |
| 5! |
| x6 |
| 7! |
| sinx |
| x |
| x2 |
| 3! |
| x4 |
| 5! |
| x6 |
| 7! |
| x2 |
| π2 |
| x2 |
| 22•π2 |
| x2 |
| n2π2 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
| π2 |
| 6 |
| π2 |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| sinx |
| x |
| x2 |
| 3! |
| x4 |
| 5! |
| x6 |
| 7! |
| sinx |
| x |
| x2 |
| 3! |
| x4 |
| 5! |
| x6 |
| 7! |
| x2 |
| π2 |
| x2 |
| 22π2 |
| x2 |
| n2π2 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
| π2 |
| 6 |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省南通中学高三(上)期中数学试卷(理科)(解析版) 题型:解答题
 展开式的各项依次记为a1(x),a2(x),a3(x),…an(x),an+1(x).
展开式的各项依次记为a1(x),a2(x),a3(x),…an(x),an+1(x).查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省宿迁中学高三(上)第二次调研数学试卷(解析版) 题型:解答题
 展开式的各项依次记为a1(x),a2(x),a3(x),…an(x),an+1(x).
展开式的各项依次记为a1(x),a2(x),a3(x),…an(x),an+1(x).查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省淮安市清江附中高三(上)第二次调研数学试卷(解析版) 题型:解答题
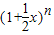 展开式的各项依次记为a1(x),a2(x),a3(x),…an(x),an+1(x).
展开式的各项依次记为a1(x),a2(x),a3(x),…an(x),an+1(x).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com