
【题目】在数列{an}中,a1=1,a2=![]() ,an+1-
,an+1-![]() an+an-1=0 (n≥2,且n∈N*),若数列{an+1+λan}是等比数列.
an+an-1=0 (n≥2,且n∈N*),若数列{an+1+λan}是等比数列.
(1)求实数λ;
(2)求数列{an}的通项公式;
(3)设![]() ,求证:
,求证: ![]() .
.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:(1)利用新数列为等比数列和递推公式,通过待定系数法进行求解;(2)利用(1)结论得到关于![]() 的方程组进行求解;(3)利用放缩法和等比数列的求和公式进行求解.
的方程组进行求解;(3)利用放缩法和等比数列的求和公式进行求解.
试题解析:(1)由数列{an+1+λan}是等比数列,可设an+1+λan=μ(an+λan-1) (n≥2).
∴an+1+(λ-μ)an-λμan-1=0,
∵an+1-![]() an+an-1=0,
an+an-1=0,
∴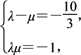 ∴λ=-
∴λ=-![]() 或λ=-3.
或λ=-3.
(2)解 由(1)知,n≥2,λ=-![]() 时,
时,
an-![]() an-1=3n-1,①
an-1=3n-1,①
n≥2,λ=-3时,an-3an-1=![]() .②
.②
由①②可得an=![]()
![]() (n≥2),当n=1时,也符合.
(n≥2),当n=1时,也符合.
∴an=![]() (3n-
(3n-![]() ),n∈N*.
),n∈N*.
(3)证明 由(2)知,
an=![]()
![]() >0,
>0,
∵an-3an-1=![]() ,∴an>3an-1,
,∴an>3an-1,
∴![]() <
<![]() ·
·![]() (n≥2).
(n≥2).
∴Sn<![]() +
+![]()
![]() =
=![]() +
+![]()
![]() -
-![]() <
<![]() +
+![]() Sn.
Sn.
∴Sn<![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】老师在四个不同的盒子里面放了4张不同的扑克牌,分别是红桃![]() ,梅花
,梅花![]() ,方片
,方片![]() 以及黑桃
以及黑桃![]() ,让明、小红、小张、小李四个人进行猜测:
,让明、小红、小张、小李四个人进行猜测:
小明说:第1个盒子里面放的是梅花![]() ,第3个盒子里面放的是方片
,第3个盒子里面放的是方片![]() ;
;
小红说:第2个盒子里面饭的是梅花![]() ,第3个盒子里放的是黑桃
,第3个盒子里放的是黑桃![]() ;
;
小张说:第4个盒子里面放的是黑桃![]() ,第2个盒子里面放的是方片
,第2个盒子里面放的是方片![]() ;
;
小李说:第4个盒子里面放的是红桃![]() ,第3个盒子里面放的是方片
,第3个盒子里面放的是方片![]() ;
;
老师说:“小明、小红、小张、小李,你们都只说对了一半.”则可以推测,第4个盒子里装的是( )
A. 红桃![]() 或黑桃
或黑桃![]() B. 红桃
B. 红桃![]() 或梅花
或梅花![]()
C. 黑桃![]() 或方片
或方片![]() D. 黑桃
D. 黑桃![]() 或梅花
或梅花![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且f(0)=0,当x>0时,
f(x)=![]() .
.
(1)求函数f(x)的解析式;
(2)解不等式f(x2-1)>-2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线y=t与曲线C:y=x(x﹣3)2的三个交点分别为A(a,t),B(b,t),C(c,t),且a<b<c.现给出如下结论:
①abc的取值范围是(0,4);
②a2+b2+c2为定值;③a+b+c=6
其中正确结论的为_______
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为对考生的月考成绩进行分析,某地区随机抽查了![]() 名考生的成绩,根据所得数据画了如下的样本频率分布直方图.
名考生的成绩,根据所得数据画了如下的样本频率分布直方图.
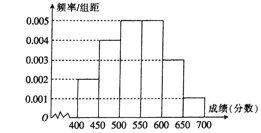
(1)求成绩在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析成绩与班级、学校等方面的关系,必须按成绩再从这![]() 人中用分层抽样方法抽取出
人中用分层抽样方法抽取出![]() 人作出进一步分析,则成绩在
人作出进一步分析,则成绩在![]() 的这段应抽多少人?
的这段应抽多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且椭圆
,且椭圆![]() 过点
过点![]() ,直线
,直线![]() 过椭圆
过椭圆![]() 的右焦点
的右焦点![]() 且与椭圆
且与椭圆![]() 交于
交于![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)已知点![]() ,求证:若圆
,求证:若圆![]() 与直线
与直线![]() 相切,则圆
相切,则圆![]() 与直线
与直线![]() 也相切.
也相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的点,且
上的点,且![]() ,沿
,沿![]() 将
将![]() 折起并连接成如图的多面体
折起并连接成如图的多面体![]() ,折后
,折后![]() .
.
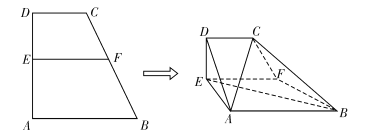
(Ⅰ)求证: ![]() ;
;
(Ⅱ)若折后直线![]() 与平面
与平面![]() 所成角
所成角![]() 的正弦值是
的正弦值是![]() ,求证:平面
,求证:平面![]() 平面
平面![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com