
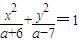 表示双曲线,命题q:圆x2+(y-1)2=9与圆(x-a)2+(y+1)2=16相交.若“¬p且q”为真命题,求实数a的取值范围.
表示双曲线,命题q:圆x2+(y-1)2=9与圆(x-a)2+(y+1)2=16相交.若“¬p且q”为真命题,求实数a的取值范围.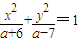 表示双曲线,则(a+6)(a-7)<0,所以p为假命题即是(a+6)(a-7)≥0;若q为真命题,则两圆心距大于两半径差的绝对值小于两半径之和,故
表示双曲线,则(a+6)(a-7)<0,所以p为假命题即是(a+6)(a-7)≥0;若q为真命题,则两圆心距大于两半径差的绝对值小于两半径之和,故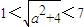 .求出它们的交集即可.
.求出它们的交集即可.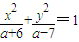 表示双曲线,
表示双曲线,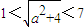 ,∴
,∴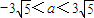 .
. 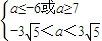 ,即
,即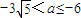 ,
,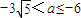 .
.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:解答题
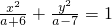 表示双曲线,命题q:圆x2+(y-1)2=9与圆(x-a)2+(y+1)2=16相交.若“¬p且q”为真命题,求实数a的取值范围.
表示双曲线,命题q:圆x2+(y-1)2=9与圆(x-a)2+(y+1)2=16相交.若“¬p且q”为真命题,求实数a的取值范围.查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省南京市外国语学校、金陵中学等四校高二(上)期中数学试卷(解析版) 题型:解答题
 表示双曲线,命题q:圆x2+(y-1)2=9与圆(x-a)2+(y+1)2=16相交.若“¬p且q”为真命题,求实数a的取值范围.
表示双曲线,命题q:圆x2+(y-1)2=9与圆(x-a)2+(y+1)2=16相交.若“¬p且q”为真命题,求实数a的取值范围.查看答案和解析>>
科目:高中数学 来源:2012-2013学年陕西省宝鸡市金台区高二(上)期末数学试卷(理科)(解析版) 题型:解答题
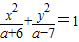 表示中心在原点,焦点在坐标轴上的双曲线,命题q:存在x∈R,则x2-4x+a<0.
表示中心在原点,焦点在坐标轴上的双曲线,命题q:存在x∈R,则x2-4x+a<0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com