
【题目】函数![]() 上任意一点
上任意一点![]() 处的切线
处的切线![]() ,在其图像上总存在异与点A的点
,在其图像上总存在异与点A的点![]() ,使得在B点处的切线
,使得在B点处的切线![]() 满足
满足![]() ,则称函数具有“自平行性”.下列有关函数
,则称函数具有“自平行性”.下列有关函数![]() 的命题:
的命题:
①函数![]() 具有“自平行性”;②函数
具有“自平行性”;②函数![]() 具有“自平行性”;
具有“自平行性”;
③函数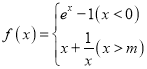 具有“自平行性”的充要条件为实数
具有“自平行性”的充要条件为实数![]() ;
;
④奇函数![]() 不一定具有“自平行性”;⑤偶函数
不一定具有“自平行性”;⑤偶函数![]() 具有“自平行性”.
具有“自平行性”.
其中所有叙述正确的命题的序号是( )
A.①③④B.①④⑤C.②③④D.①②⑤
科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() =1(a>0,b>0)的左右焦点为F1,F2过点F1的直线l与双曲线C的左支交于AB两点,△BF1F2的面积是△AF1F2面积的三倍,∠F1AF2=90°,则双曲线C的离心率为( )
=1(a>0,b>0)的左右焦点为F1,F2过点F1的直线l与双曲线C的左支交于AB两点,△BF1F2的面积是△AF1F2面积的三倍,∠F1AF2=90°,则双曲线C的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某工厂每天固定成本是4万元,每生产一件产品成本增加100元,工厂每件产品的出厂价定为![]() 元时,生产
元时,生产![]() 件产品的销售收入是
件产品的销售收入是![]() (元),
(元),![]() 为每天生产
为每天生产![]() 件产品的平均利润(平均利润=总利润/总产量).销售商从工厂每件
件产品的平均利润(平均利润=总利润/总产量).销售商从工厂每件![]() 元进货后又以每件
元进货后又以每件![]() 元销售,
元销售, ![]() ,其中
,其中![]() 为最高限价
为最高限价![]() ,
, ![]() 为销售乐观系数,据市场调查,
为销售乐观系数,据市场调查, ![]() 是由当
是由当![]() 是
是![]() ,
, ![]() 的比例中项时来确定.
的比例中项时来确定.
(1)每天生产量![]() 为多少时,平均利润
为多少时,平均利润![]() 取得最大值?并求
取得最大值?并求![]() 的最大值;
的最大值;
(2)求乐观系数![]() 的值;
的值;
(3)若![]() ,当厂家平均利润最大时,求
,当厂家平均利润最大时,求![]() 与
与![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,下述四个结论:
,下述四个结论:
①![]() 是偶函数;
是偶函数;
②![]() 的最小正周期为
的最小正周期为![]() ;
;
③![]() 的最小值为0;
的最小值为0;
④![]() 在
在![]() 上有3个零点
上有3个零点
其中所有正确结论的编号是( )
A.①②B.①②③C.①③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() (a>b>0)的左焦点为F,上顶点为B. 已知椭圆的离心率为
(a>b>0)的左焦点为F,上顶点为B. 已知椭圆的离心率为![]() ,点A的坐标为
,点A的坐标为![]() ,且
,且![]() .
.
(I)求椭圆的方程;
(II)设直线l: ![]() 与椭圆在第一象限的交点为P,且l与直线AB交于点Q. 若
与椭圆在第一象限的交点为P,且l与直线AB交于点Q. 若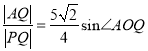 (O为原点) ,求k的值.
(O为原点) ,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《汉字听写大会》不断创收视新高,为了避免“书写危机”,弘扬传统文化,某市大约10万名市民进行了汉字听写测试.现从某社区居民中随机抽取50名市民的听写测试情况,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第1组![]() ,第2组
,第2组![]() ,…,第6组
,…,第6组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.

(1)若电视台记者要从抽取的市民中选1人进行采访,求被采访人恰好在第2组或第6组的概率;
(2)试估计该市市民正确书写汉字的个数的众数与中位数;
(3)已知第4组市民中有3名男性,组织方要从第4组中随机抽取2名市同组成弘扬传统文化宣传队,求至少有1名女性市民的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com