
【题目】已知函数 ![]() .
.
(1)判断并证明f(x)的奇偶性;
(2)求证: ![]() ;
;
(3)已知a,b∈(﹣1,1),且 ![]() ,
, ![]() ,求f(a),f(b)的值.
,求f(a),f(b)的值.
【答案】
(1)
解:由 ![]() 可得函数的定义域(﹣1,1),关于原点对称
可得函数的定义域(﹣1,1),关于原点对称
∵ ![]() =
= ![]() 故函数f(x)为奇函数
故函数f(x)为奇函数
(2)
解:∵f(a)+f(b)= ![]() =
= ![]()
![]() =
= 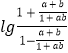 =
= ![]()
∴ ![]()
(3)
解:∵ ![]() =1
=1
∴f(a)+f(b)=1 ![]() =2
=2
∴f(a)+f(﹣b)=2
∵f(﹣b)=﹣f(b),
∴f(a)﹣f(b)=2,解得: ![]()
【解析】(1)由 ![]() 可得函数的定义域(﹣1,1),关于原点对称,再由
可得函数的定义域(﹣1,1),关于原点对称,再由 ![]() =
= ![]() 可判断函数奇偶性(2)分别计算 f(a)+f(b)与
可判断函数奇偶性(2)分别计算 f(a)+f(b)与 ![]() 可证(3)由(2)
可证(3)由(2) ![]() 可得f(a)+f(b)=1
可得f(a)+f(b)=1 ![]() ,f(a)+f(b)=2结合奇函数的性质可得f(﹣b)=﹣f(b),从而可求
,f(a)+f(b)=2结合奇函数的性质可得f(﹣b)=﹣f(b),从而可求
【考点精析】根据题目的已知条件,利用函数奇偶性的性质的相关知识可以得到问题的答案,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.


科目:高中数学 来源: 题型:
【题目】如图,已知海岛A到海岸公路BC的距离AB=50km,B,C间的距离为100km,从A到C必须先坐船到BC上的某一点D,航速为25km/h,再乘汽车到C,车速为50km/h,记∠BDA=θ
(1)试将由A到C所用的时间t表示为θ的函数t(θ);
(2)问θ为多少时,由A到C所用的时间t最少?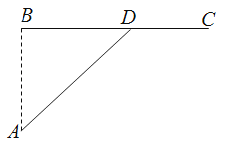
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家具厂生产一种课桌,每张课桌的成本为50元,出厂单价定为80元,该厂为鼓励销售商多订购,决定一次订购量超过100张时,每超过一张,这批订购的全部课桌出厂单价降低0.02元.根据市场调查,销售商一次订购量不会超过1000张.
(1)设一次订购量为x张,课桌的实际出厂单价为P元,求P关于x的函数关系式P(x);
(2)当一次订购量x为多少时,该家具厂这次销售课桌所获得的利润f(x)最大?其最大利润是多少元?(家具厂售出一张课桌的利润=实际出厂单价﹣成本).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》有如下问题:“今有蒲(水生植物名)生一日,长三尺;莞(植物名,俗称水葱、席子草)生一日,长一尺.蒲生日自半,莞生日自倍.问几何日而长等?”意思是:今有蒲生长1日,长为3尺;莞生长1日,长为1尺.蒲的生长逐日减半,莞的生长逐日增加1倍.若蒲、莞长度相等,则所需的时间约为( )(结果保留一位小数.参考数据:![]() ,
,![]() )( )
)( )
A. 1.3日 B. 1.5日 C. 2.6日 D. 2.8日
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别是a,b,c,已知2cosA(bcosC+ccosB)=a.
(1)求角A;
(2)若a= ![]() ,b+c=5,求△ABC的面积.
,b+c=5,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
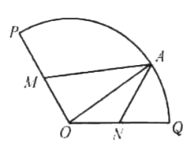
【题目】某校有一块圆心![]() ,半径为200米,圆心角为
,半径为200米,圆心角为![]() 的扇形绿地
的扇形绿地![]() ,半径
,半径![]() 的中点分别为
的中点分别为![]() ,
,![]() 为弧
为弧![]() 上的一点,设
上的一点,设![]() ,如图所示,拟准备两套方案对该绿地再利用.
,如图所示,拟准备两套方案对该绿地再利用.
(1)方案一:将四边形绿地![]() 建成观赏鱼池,其面积记为
建成观赏鱼池,其面积记为![]() ,试将
,试将![]() 表示为关于
表示为关于![]() 的函数关系式,并求
的函数关系式,并求![]() 为何值时,
为何值时,![]() 取得最大?
取得最大?
(2)方案二:将弧![]() 和线段
和线段![]() 围成区域建成活动场地,其面积记为
围成区域建成活动场地,其面积记为![]() ,试将
,试将![]() 表示为关于
表示为关于![]() 的函数关系式;并求
的函数关系式;并求![]() 为何值时,
为何值时,![]() 取得最大?
取得最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() 分别为等差数列和等比数列,
分别为等差数列和等比数列, ![]() ,
, ![]() 的前
的前![]() 项和为
项和为![]() .函数
.函数![]() 的导函数是
的导函数是![]() ,有
,有![]() ,且
,且![]() 是函数
是函数![]() 的零点.
的零点.
(1)求![]() 的值;
的值;
(2)若数列![]() 公差为
公差为![]() ,且点
,且点![]() ,当
,当![]() 时所有点都在指数函数
时所有点都在指数函数![]() 的图象上.
的图象上.
请你求出![]() 解析式,并证明:
解析式,并证明: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com