
【题目】已知圆![]() .(14分)
.(14分)
(1)此方程表示圆,求m的取值范围;
(2)若(1)中的圆与直线x+2y-4=0相交于M、N两点,且![]() (O为坐标原点),求m的值;
(O为坐标原点),求m的值;
(3)在(2)的条件下,求以![]() 为直径的圆的方程.
为直径的圆的方程.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
试题分析:(1)把方程![]() 化为圆的标准方程为
化为圆的标准方程为![]() ,故有
,故有![]() ,由此解得
,由此解得![]() 的范围.
的范围.
(2)由直线方程与圆的方程联立消![]() ,把直线
,把直线![]() 代入圆的方程化简到关于
代入圆的方程化简到关于![]() 的二次方程,设
的二次方程,设![]() .∵
.∵![]() ,故
,故 ![]() ①,利用根与系数的关系可得
①,利用根与系数的关系可得![]() ,
,![]() ,代入①求得
,代入①求得![]() 的值.
的值.
(3)由(2)可以求出![]() 两点的坐标,由两点间距离公式可以求出线段
两点的坐标,由两点间距离公式可以求出线段![]() 的长度,再由中点公式可以求出圆心.可以得到以
的长度,再由中点公式可以求出圆心.可以得到以![]() 直径的圆的方程.当然也可以圆的直径式
直径的圆的方程.当然也可以圆的直径式![]() 直接写出圆的方程.
直接写出圆的方程.
试题解析:
(1)方程![]() ,可化为
,可化为
![]() ,
,
∵此方程表示圆,
∴![]() ,即
,即![]() .
.
(2)
消去![]() 得
得![]() ,
,
化简得![]() .
.
设![]() ,则
,则
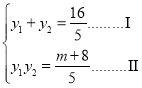
由![]() 得
得![]()
即![]() ,
,
∴![]() .
.
将![]() 两式代入上式得
两式代入上式得
![]() ,
,
解之得![]() .
.
(3)由![]() ,代入
,代入![]() ,
,
化简整理得![]() ,解得
,解得![]() .
.
∴![]() .
.
∴![]() ,
,
∴![]() 的中点C的坐标为
的中点C的坐标为![]() .
.
又![]() ,
,
∴所求圆的半径为![]() .
.
∴所求圆的方程为![]() .
.


科目:高中数学 来源: 题型:
【题目】下面给出四种说法:
①用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好;
②命题P:“x0∈R,x02﹣x0﹣1>0”的否定是¬P:“x∈R,x2﹣x﹣1≤0”;
③设随机变量X服从正态分布N(0,1),若P(x>1)=p则P(﹣1<X<0)=![]() ﹣p
﹣p
④回归直线一定过样本点的中心(![]() ).
).
其中正确的说法有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=60°。
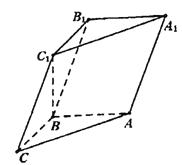
(Ⅰ)求证:C1B⊥平面ABC;
(Ⅱ)设![]() (0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,试求λ的值.
(0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,试求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B、C是△ABC的三个内角,向量m=(-1, ![]() ),n=(cosA,sinA),且m·n=1.
),n=(cosA,sinA),且m·n=1.
(1)求角A;
(2)若![]() =-3,求tanC.
=-3,求tanC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方形ABCD和正方形ABEF的边长都是1,并且平面ABCD⊥平面ABEF,点M在AC上移动,点N在BF上移动.若|CM|=|BN|=a(0<a<![]() ).
).
(1)求MN的长度;
(2)当a为何值时,MN的长度最短.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次国际学术会议上,来自四个国家的五位代表被安排坐在一张圆桌,为了使他们能够自由交谈,事先了解到的情况如下:
甲是中国人,还会说英语.
乙是法国人,还会说日语.
丙是英国人,还会说法语.
丁是日本人,还会说汉语.
戊是法国人,还会说德语.
则这五位代表的座位顺序应为( )
A. 甲丙丁戊乙 B. 甲丁丙乙戊
C. 甲乙丙丁戊 D. 甲丙戊乙丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)的定义域为A,若x1,x2∈A且f(x1)=f(x2)时总有x1=x2,则称f(x)为单函数,例如,函数f(x)=2x+1(x∈R)是单函数.下列命题:
①函数f(x)=x2(x∈R)是单函数;
②函数f(x)=![]() 是单函数;
是单函数;
③若f(x)为单函数,x1,x2∈A且x1≠x2,则f(x1)≠f(x2);
④在定义域上具有单调性的函数一定是单函数.
其中的真命题是________.(写出所有真命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com