
【题目】已知结论:“在正三角形ABC中,若D是边BC的中点,G是三角形ABC的重心,则 ![]() ”,若把该结论推广到空间,则有结论:“在棱长都相等的四面体ABCD中,若△BCD的中心为M,四面体内部一点O到四面体各面的距离都相等,则
”,若把该结论推广到空间,则有结论:“在棱长都相等的四面体ABCD中,若△BCD的中心为M,四面体内部一点O到四面体各面的距离都相等,则 ![]() =( )
=( )
A.1
B.2
C.3
D.4
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的焦距为2,且过点P(1,
=1(a>b>0)的焦距为2,且过点P(1, ![]() )
)
(1)椭圆C的方程;
(2)设椭圆C的左右焦点分别为F1 , F2 , 过点F2的直线l与椭圆C交于M,N两点.
①当直线l的倾斜角为45°时,求|MN|的长;
②求△MF1N的内切圆的面积的最大值,并求出当△MF1N的内切圆的面积取最大值时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】连江一中第49届田径运动会提出了“我运动、我阳光、我健康、我快乐”的口号,某同学要设计一张如图所示的竖向张贴的长方形海报进行宣传,要求版心面积为162dm2(版心是指图中的长方形阴影部分,dm为长度单位分米),上、下两边各空2dm,左、右两边各空1dm. 
(1)若设版心的高为xdm,求海报四周空白面积关于x的函数S(x)的解析式;
(2)要使海报四周空白面积最小,版心的高和宽该如何设计?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,CD=1,∠BCD=60°,BD⊥CD,正方形ADEF,且面ADEF⊥面ABCD. 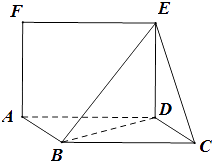
(Ⅰ)求证:BD⊥平面ECD.
(Ⅱ)求D点到面CEB的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,设角A,B,C的对边分别为a,b,c,向量 ![]() =(cosA,sinA),
=(cosA,sinA), ![]() =(
=( ![]() ﹣sinA,cosA),若
﹣sinA,cosA),若 ![]()
![]() =1.
=1.
(1)求角A的大小;
(2)若b=4 ![]() ,且c=
,且c= ![]() a,求△ABC的面积.
a,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产一种机器的固定成本为5000元,且每生产100部,需要加大投入2500元.对销售市场进行调查后得知,市场对此产品的需求量为每年500部,已知销售收入函数为 ![]() ,其中x是产品售出的数量0≤x≤500.
,其中x是产品售出的数量0≤x≤500.
(1)若为x年产量,y表示利润,求y=f(x)的解析式
(2)当年产量为何值时,工厂的年利润最大?其最大值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)的定义域为{x|x∈R,且x≠2},且y=f(x+2)是偶函数,当x<2时,f(x)=|2x﹣1|,那么当x>2时,函数f(x)的递减区间是( )
A.(3,5)
B.(3,+∞)
C.(2,+∞)
D.(2,4]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com