
| π |
| 12 |
| π |
| 4 |
| MP |
| MQ |
| PQ |
A、f(
| ||||
B、f(
| ||||
C、f(
| ||||
D、f(-
|
| MP |
| MQ |
| PQ |
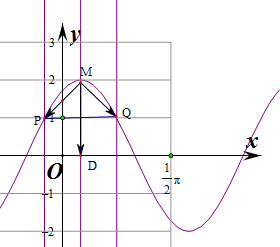 解:∵若f(x)图象上存在一个最高点M,使得(
解:∵若f(x)图象上存在一个最高点M,使得(| MP |
| MQ |
| PQ |
| MP |
| MQ |
-
| ||||
| 2 |
| π |
| 12 |
| π |
| 12 |
| π |
| 12 |


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
| ||
| 2 |
| π |
| 4 |
| A、①的逆否命题为真 |
| B、②的否命题为真 |
| C、③的否命题为假 |
| D、④的逆命题为假 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某天甲、乙两同学约好在晚上8点到9点之间在某地会面,假定两人到达指定地点的时刻是等可能的且相互独立的,并约定先到者等待后到者时间是15分钟,之后就可以离去,问两人能够见面的概率有多大?
某天甲、乙两同学约好在晚上8点到9点之间在某地会面,假定两人到达指定地点的时刻是等可能的且相互独立的,并约定先到者等待后到者时间是15分钟,之后就可以离去,问两人能够见面的概率有多大?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com