
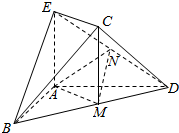
 如图,在几何体ABDCE中,AB=AD,AE⊥平面ABD,M为线段BD的中点,MC∥AE,AE=MC.
如图,在几何体ABDCE中,AB=AD,AE⊥平面ABD,M为线段BD的中点,MC∥AE,AE=MC.分析 (1)先证明AM⊥BD,MC⊥AM,从而AM⊥平面CBD,再由EC⊥平面CBD,能证明平面BCD⊥平面CDE.
(2)由三角形中位线定理得MN∥BE,再由EC∥AM,能证明平面AMN∥平面BEC.
解答 证明:(1)∵AB=AD,M为线段BD的中点,∴AM⊥BD.
∵AE⊥平面ABD,MC∥AE,∴MC⊥平面ABD.
∴MC⊥AM,∴AM⊥平面CBD.
又MC∥AE,MC=AE,∴四边形AMCE为平行四边形,
∴EC∥AM,∴EC⊥平面CBD,
∴平面BCD⊥平面CDE.
(2)∵M为BD中点,N为ED中点,
∴MN∥BE
由(1)知,EC∥AM且AM∩MN=M,BE∩EC=E,
∴平面AMN∥平面BEC.
点评 本题考查面面垂直、面面平行的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:解答题
 已知PQ与圆O相切于点A,直线PBC交圆于B、C两点,D是圆上一点,且AB∥DC,DC的延长线交PQ于点Q.
已知PQ与圆O相切于点A,直线PBC交圆于B、C两点,D是圆上一点,且AB∥DC,DC的延长线交PQ于点Q.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校在2015年11月份的高三期中考试后,随机地抽取了50名学生的数学成绩并进行了分析,结果这50名同学的成绩全部介于80分到140分之间.现将结果按如下方式分为6组,第一组[80,90),第二组[90,100),…,第六组[130,140],得到如图所示的频率分布直方图.
某校在2015年11月份的高三期中考试后,随机地抽取了50名学生的数学成绩并进行了分析,结果这50名同学的成绩全部介于80分到140分之间.现将结果按如下方式分为6组,第一组[80,90),第二组[90,100),…,第六组[130,140],得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com