
����Ŀ��ij����վΪ�˿���ij������ҩ��Ԥ�����R����Ч��������С����������飬�õ����¶�ʧ���ݵ�![]() ������
������
���� | δ���� | �ܼ� | |
û����ҩ | 20 | 30 | 50 |
����ҩ |
|
| 50 |
�ܼ� |
|
| 100 |
���û����ҩ��С��������ȡ��ֻ��δ�����Ķ�����Ϊ![]() ���ӷ���ҩ���С��������ȡ��ֻ��δ�����Ķ�����Ϊ
���ӷ���ҩ���С��������ȡ��ֻ��δ�����Ķ�����Ϊ![]() ���õ����±�����ϵ��
���õ����±�����ϵ��![]()
��1�����![]() ������������
������������![]() ��
��![]() ��
��![]() ��
��![]() ��ֵ
��ֵ
��2���Ƿ���![]() �İ�����Ϊҩ����Ч����˵������
�İ�����Ϊҩ����Ч����˵������
���ο���ʽ��![]() ����
����![]() ʱ����
ʱ����![]() �İ�����ΪA��B�йأ�
�İ�����ΪA��B�йأ�![]() ʱ����
ʱ����![]() �İ�����ΪA��B�йأ�
�İ�����ΪA��B�йأ�

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]()
��1��������ͼ���ڵ�![]() �������߷��̣�
�������߷��̣�
��2����![]() ʱ����֤��
ʱ����֤��![]() ��
��
��3����![]() �������
�������![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ʒ�۸������Ʒ��������֮��ļ�������������±���

��1������ڵ����Իع鷽�̣�
��2�����ã�1���еĻع鷽�̣����۸�![]() Ԫ
Ԫ![]() ʱ����������
ʱ����������![]() ��Ԥ��ֵΪ���٣�
��Ԥ��ֵΪ���٣�
�ο���ʽ�����Թ�ط��̣� ![]() ������
������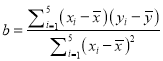 ��
�� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��λ����10��Ա��������ij����������±���
Ա����� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
��н����Ԫ�� | 4 | 4.5 | 6 | 5 | 6.5 | 7.5 | 8 | 8.5 | 9 | 51 |
��1����õ�λԱ��������н��ƽ��ֵ����λ����
��2���Ӹõ�λ����ȡ2�ˣ���2������н�������7���������Ϊ![]() ����
����![]() �ķֲ��к�������
�ķֲ��к�������
��3����֪Ա����н�����빤����������ع�ϵ��ijԱ��������һ�������������н�ֱ�Ϊ4��Ԫ��5.5��Ԫ��6��Ԫ��8.5��Ԫ��Ԥ���Ա�����������нΪ���٣�
�������Իع鷽��![]() ��ϵ�����㹫ʽ�ֱ�Ϊ��
��ϵ�����㹫ʽ�ֱ�Ϊ��
 ��
�� ![]() ������
������![]() Ϊ������ֵ.
Ϊ������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ӹ�˾����һ�������ֻ��������ÿ������ijɱ���15Ԫ�����ۼ���20Ԫ����ƽ������![]() ����ͨ���Ľ����գ�ÿ������ijɱ����䣬�����ͼ�����������ߣ��г������Ľ�����������ÿ����������ۼ���ߵİٷ���Ϊ
����ͨ���Ľ����գ�ÿ������ijɱ����䣬�����ͼ�����������ߣ��г������Ľ�����������ÿ����������ۼ���ߵİٷ���Ϊ![]() ����ô��ƽ�����������ٵİٷ���Ϊ
����ô��ƽ�����������ٵİٷ���Ϊ![]() ���ǸĽ����պ���ӹ�˾���۸��������ƽ��������
���ǸĽ����պ���ӹ�˾���۸��������ƽ��������![]() ��Ԫ��.
��Ԫ��.
��1���![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2���Ľ����պ���ȷ���������ֻ�������ۼۣ�ʹ���ӹ�˾���۸��������ƽ���������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
(1)���ۺ���![]() �ĵ����ԣ�
�ĵ����ԣ�
(2)��![]() ʱ,��
ʱ,��![]() �ļ���ֵΪ
�ļ���ֵΪ![]() ,��СֵΪ
,��СֵΪ![]() ,��
,��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������
������![]() �ڵ�
�ڵ�![]() ��������ƽ����
��������ƽ����![]() �ᣮ
�ᣮ
��1����![]() �ĵ������䣻
�ĵ������䣻
��2��֤������![]() ʱ��
ʱ�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ȫ��U=R������A={x|2x+a��0}��B={x|x2��2x��3��0}�� ����a=2ʱ����A��B��
������A�ɣ�UB��=����ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() ,��
,��![]() ��Բ
��Բ![]() �ϵ�����һ��,���߶�
�ϵ�����һ��,���߶�![]() �Ĵ�ֱƽ������ֱ��
�Ĵ�ֱƽ������ֱ��![]() ���ڵ�
���ڵ�![]() .
.
��1����![]() ��Ĺ켣���̣�
��Ĺ켣���̣�
��2����ֱ��![]() ���
���![]() �Ĺ켣���У�����Բ
�Ĺ켣���У�����Բ![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��![]() ����ֱ��
����ֱ��![]() ��������
��������![]() �������
�������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com