练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．已知函数f（x） 在R上满足f（x）=2f（2-x）-x2+8x-8，则曲线y=f（x）在点（1，f（1））处的切线方程是（　　）
    A．y=-2x+3B．y=2x-1C．y=-6x+7D．y=3x-2

    分析 取x=1，可求出f（1）=1．对函数f（x）求导，得f'（x）=-2f'（2-x）-2x+8，再取x=1得曲线y=f（x）在点（1，f（1））处的切线斜率为f'（1）=2，最后用直线方程的点斜率式，可得所求的切线方程．

    解答 解：取x=1，得f（1）=2f（1）-1，可得f（1）=1．
    对函数f（x）求导，得f'（x）=-2f'（2-x）-2x+8，
    ∴f'（1）=-2f'（1）+6，得f'（1）=2
    由此可得曲线y=f（x）在点（1，f（1））处的切线斜率k=2
    ∴所求切线方程为y-1=2（x-1），化简得y=2x-1
    故选：B．

    点评 本题给出定义在R上的复合形式的函数，求函数图象在x=1处的切线方程，着重考查了导数的运算法则和导数几何意义等知识点，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    18．函数f（x）=$\frac{{x}^{2}•{e}^{ln\frac{1}{2016}}}{{e}^{x}}$的大致图象为（　　）
    A．B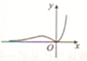．C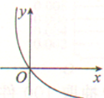．D．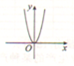

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．若2a+2b=1，ab＞0，则$\frac{1}{a}$+$\frac{1}{b}$的最小值是（　　）
    A．4B．8C．12D．16

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知命题：若数列{an}为等差数列，且am=k，an=l（m≠n，m，n∈N+），则am+n=$\frac{ln-km}{n-m}$，现已知等比数列{bn}（bn＞0，n∈N+），bm=a，bn=b（m≠n，m，n∈N+）若类比上述结论，则可得到bm+n（　　）
    A．$\root{n-m}{\frac{{b}^{n}}{{a}^{m}}}$B．$\frac{{b}^{n}-{a}^{m}}{n-m}$C．$\root{n-m}{{b}^{n}-{a}^{m}}$D．$\frac{\frac{{b}^{n}}{{a}^{m}}}{n-m}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．函数f（x）=lg（-x2+2x+15）的定义域为（　　）
    A．（-5，3）B．（-3，5）C．（-∞，-3）∪（5，+∞）D．（-∞，-5）∪（3，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．函数 y=$\frac{2}{2sinx-1}$的值域是（　　）
    A．（-∞，-$\frac{2}{3}$]∪[2，+∞）B．[-$\frac{2}{3}$，2]C．[-$\frac{2}{3}$，0）∪（0，2]D．（-∞，0）∪（0，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知函数f（x）=x2+$\frac{2{a}^{3}}{x}$+1．
    （Ⅰ）若曲线y=f（x）在点（1，f（1））处的切线与直线y=1平行，求a的值；
    （Ⅱ）若0＜a＜2，求函数f（x）在区间[1，2]上的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

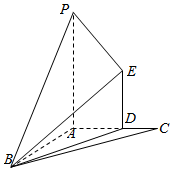    8．平面外ABC的一点P，AP、AB、AC两两互相垂直，过AC的中点D做ED⊥面ABC，且ED=1，PA=2，AC=2，连接BP，BE，多面体B-PADE的体积是$\frac{\sqrt{3}}{3}$；
    （1）画出面PBE与面ABC的交线，说明理由；
    （2）求面PBE与面ABC所成的锐二面角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知某个长方形的面积为a2-（b+1）2，且它的边长都是整式，则它的周长为（　　）
    A．2aB．2a2-2b2-4bC．4a或2a2-2b2-4bD．以上都不对

    查看答案和解析>>

    同步练习册答案