(本题满分12分)定义:
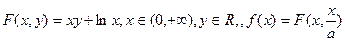
(其中
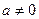
)。
(1)求
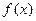
的单调区间;
(2)若
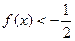
恒成立,试求实数
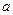
的取值范围;
(1)
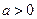
时,
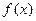
增区间为
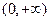
;
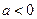
时,
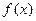
增区间为
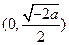
,减区间为
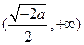
.
(2)
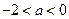
解:(1)
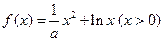
,则
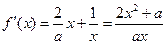
………1分
①当
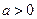
时,
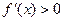
对
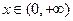
恒成立,
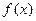
在
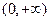
上递增
②当
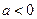
时,令
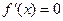
,则
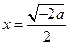
, ………3分
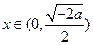
时,
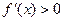
,
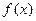
为增函数;
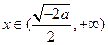
时,
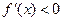
,
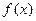
为减函数
综上,
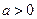
时,
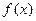
增区间为
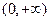
;
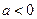
时,
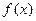
增区间为
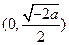
,减区间为
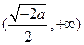
. ………6分
(2)由(1)知
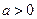
时,
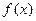
在
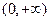
递增,
且
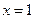
时,
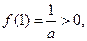
则
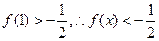
不恒成立,故
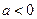
………8分
又
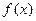
的极大值即
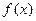
最大值
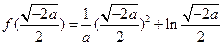
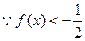
恒成立,只须
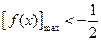
∴
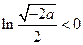
,即
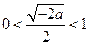
∴
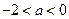
………12分
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(本小题满分

12分)
已知定义域为
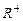
的函数
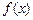
具有以下性质

:①
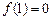
,
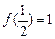
;②
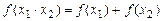
;③当
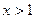
时,总有
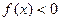
,
(1)求
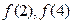
;
(2)求不等式
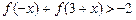
的解集
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
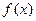
的定义域为R,若存在常数
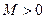
,使
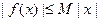
对一切实数
x均成立,则称
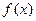
为F函数。现给出下列函数:
①
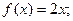
②
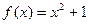
;
③
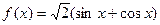
;④
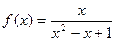
;
⑤
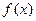
是定义在实数集R上的奇函数,且对一切

其中是F函数的函数有
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
设函数
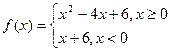
则不等式
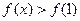
的解集是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知函数
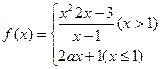
,在点
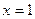
处连续,则
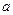
的值是 ( )
A.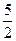 | B.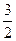 | C.2 | D.3 |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知
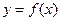
是偶函数,当
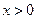
时,
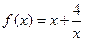
,当
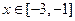
时,
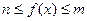
恒成立,则
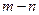
的最小值是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
如果函数
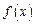
满足:对任意实数
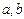
都有
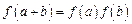
,且
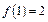
,
则
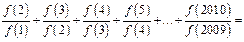
_____________________.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知函数
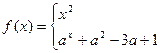
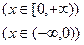
在区间
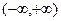
是增函数,则常数
a的取值范围是
| A.1≤a≤2 | B.a<1或a≥2 | C.1<a≤2 | D.a<1或a>2 |
查看答案和解析>>

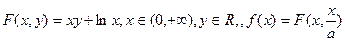 (其中
(其中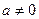 )。
)。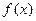 的单调区间;
的单调区间;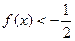 恒成立,试求实数
恒成立,试求实数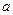 的取值范围;
的取值范围; 小学教材全测系列答案
小学教材全测系列答案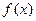 的定义域为R,若存在常数
的定义域为R,若存在常数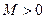 ,使
,使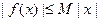 对一切实数x均成立,则称
对一切实数x均成立,则称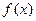 为F函数。现给出下列函数:
为F函数。现给出下列函数: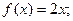 ②
②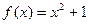 ;
;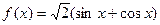 ;④
;④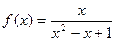 ;
;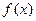 是定义在实数集R上的奇函数,且对一切
是定义在实数集R上的奇函数,且对一切 