
【题目】已知椭圆![]() ,定义椭圆
,定义椭圆![]() 上的点
上的点![]() 的“伴随点”为
的“伴随点”为![]() .
.
(1)求椭圆![]() 上的点
上的点![]() 的“伴随点”
的“伴随点”![]() 的轨迹方程;
的轨迹方程;
(2)如果椭圆![]() 上的点
上的点![]() 的“伴随点”为
的“伴随点”为![]() ,对于椭圆
,对于椭圆![]() 上的任意点
上的任意点![]() 及它的“伴随点”
及它的“伴随点”![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)当![]() ,
, ![]() 时,直线
时,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,若点
两点,若点![]() ,
, ![]() 的“伴随点”分别是
的“伴随点”分别是![]() ,
, ![]() ,且以
,且以![]() 为直径的圆经过坐标原点
为直径的圆经过坐标原点![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3) ![]() .
.
【解析】试题分析:(1)利用相关点代入法求解;(2)先由已知求得椭圆方程为![]() ,设
,设![]()
![]()
![]()
![]() ;(3)设
;(3)设![]() , 1)当直线
, 1)当直线![]() 的斜率存在时,设方程为
的斜率存在时,设方程为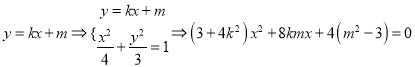
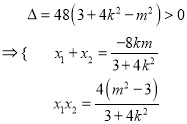 ,由以
,由以![]() 为直径的圆经过原点
为直径的圆经过原点![]()
![]()
![]()
![]() ,又
,又![]() 到直线的距离
到直线的距离![]() ;2) 当直线
;2) 当直线![]() 的斜率不存在时,设方程为
的斜率不存在时,设方程为
![]()
![]() 的面积是定值
的面积是定值![]() .
.
试题解析:(1)解.设![]() (
(![]() )由题意
)由题意 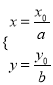 则
则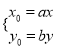 ,又
,又![]()
![]()
![]() ,从而得
,从而得![]()
(2)由![]() ,得
,得![]() .又
.又![]() ,得
,得![]() .
.
![]() 点
点![]() 在椭圆上,
在椭圆上, ![]() ,
, ![]() ,且
,且![]() ,
,
![]()
![]() ,
,
由于![]() ,
, ![]() 的取值范围是
的取值范围是![]()
(3) 设![]() ,则
,则![]() ;
;
1)当直线![]() 的斜率存在时,设方程为
的斜率存在时,设方程为![]() , 由
, 由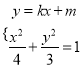
得![]() ; 有
; 有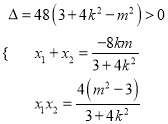 ①
①
由以![]() 为直径的圆经过坐标原点O可得:
为直径的圆经过坐标原点O可得: ![]() ;
;
整理得: ![]() ②
②
将①式代入②式得: ![]() ,
,
![]()
又点![]() 到直线
到直线![]() 的距离
的距离![]()
![]()
所以![]()
2) 当直线![]() 的斜率不存在时,设方程为
的斜率不存在时,设方程为![]()
联立椭圆方程得![]() ;代入
;代入![]() 得
得![]() ,解得
,解得![]() ,从而
,从而![]() ,
,![]() 综上:
综上: ![]() 的面积是定值
的面积是定值![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列各组函数中表示同一函数的是( )
①f(x)= ![]() 与g(x)=x
与g(x)=x ![]()
②f(x)=|x|与g(x)= ![]()
③f(x)=x0与g(x)= ![]()
④f(x)=x2﹣2x﹣1与g(t)=t2﹣2t﹣1.
A.①③
B.②③
C.③④
D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
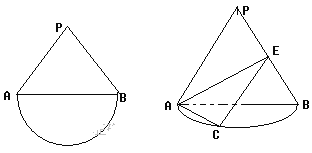
【题目】如图是一个边长为![]() 的正三角形和半圆组成的图形,现把
的正三角形和半圆组成的图形,现把![]() 沿直线AB折起使得与圆所在平面垂直,已知点C是半圆的一个三等分点(靠左边一点),点E是线段PB上的点,(1)当点E是PB的中点时,在圆弧上找一点Q,使得
沿直线AB折起使得与圆所在平面垂直,已知点C是半圆的一个三等分点(靠左边一点),点E是线段PB上的点,(1)当点E是PB的中点时,在圆弧上找一点Q,使得![]() 平面
平面![]() ;(2)当二面角
;(2)当二面角![]() 的正切值为
的正切值为![]() 时,求BE的长。
时,求BE的长。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲厂根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品x(百台),其总成本为G(x)(万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本),销售收入R(x)(万元)满足R(x)= ![]() ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)写出利润函数y=f(x)的解析式(利润=销售收入﹣总成本);
(2)要使甲厂有盈利,求产量x的范围;
(3)甲厂生产多少台产品时,可使盈利最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F1,F2分别是椭圆E: ![]() (a>b>0)的左、右焦点,过点F1的直线交椭圆E于A,B两点,|AF1|=3|BF1|,若cos∠AF2B=
(a>b>0)的左、右焦点,过点F1的直线交椭圆E于A,B两点,|AF1|=3|BF1|,若cos∠AF2B=![]() ,则椭圆E的离心率为( )
,则椭圆E的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知焦距为2的椭圆W: ![]() (a>b>0)的左、右焦点分别为A1,A2,上、下顶点分别为B1,B2,点M(x0,y0)为椭圆W上不在坐标轴上的任意一点,且四条直线MA1,MA2,MB1,MB2的斜率之积为
(a>b>0)的左、右焦点分别为A1,A2,上、下顶点分别为B1,B2,点M(x0,y0)为椭圆W上不在坐标轴上的任意一点,且四条直线MA1,MA2,MB1,MB2的斜率之积为![]() .
.
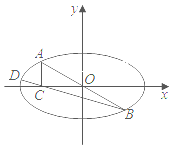
(1)求椭圆W的标准方程;
(2)如图所示,点A,D是椭圆W上两点,点A与点B关于原点对称,AD⊥AB,点C在x轴上,且AC与x轴垂直,求证:B,C,D三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
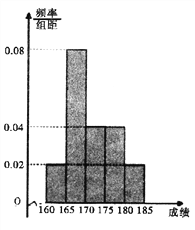
【题目】近期中央电视台播出的《中国诗词大会》火遍全国.某选拔赛后,随机抽取100名选手的成绩,按成绩由低到高依次分为第1,2,3,4,5组,制成频率分布直方图如下图所示:
(I)在第3、4、5组中用分层抽样抽取5名选手,求第3、4、5组每组各抽取多少名选手;
(II)在(I)的前提下,在5名选手中随机抽取2名选手,求第4组至少有一名选手被抽取的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公园有一个直角三角形地块,现计划把它改造成一块矩形和两块三角形区域.如图,矩形区域用于娱乐城设施的建设,三角形BCD区域用于种植甲种观赏花卉,三角形CAE区域用于种植乙种观赏花卉.已知OA=4千米,OB=3千米,∠AOB=90°,甲种花卉每平方千米造价1万元,乙种花卉每平方千米造价4万元,设OE=x千米.试建立种植花卉的总造价为y(单位:万元)关于x的函数关系式;求x为何值时,种植花卉的总造价最小,并求出总造价. 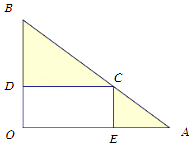
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com