
已知函数f (x ) = ax2 + bx + c与函数g (x ) =-bx,(a、b、c∈R),若a>b>c且a + b + c = 0.
(I)证明:方程f (x ) = g (x )有两个不等实根;
(II)用反证法证明:-2<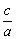 <
<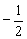 .
.
证明:(1)证明由ax2 + bx + c =-bx得ax2 + 2bx + c = 0. ①………2分
∵ a>b>c且a + b + c = 0.
∴ a>0,b =-(a + c). ………4分
△= 4b2-4ac = 4 (a + c)2-4ac = 4[(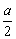 + c)2 +
+ c)2 +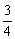 a2]>0. ………6分
a2]>0. ………6分
∴ ①有两个不相等的实数根,即方程f (x ) = g (x )有两个不等实根………8分
(2)证明:若结论不成立,则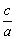 ≤-2或
≤-2或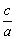 ≥-
≥-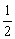 .………10分
.………10分
由(1)可知a>0,∴ c≤-2a或2c≥-a,………12分
即 a + c≤-a或a + c≥-c,由于a + c =-b. ………13分
∴ a≤b≤c与已知条件a>b>c相矛盾,故原命题成立………14分.


科目:高中数学 来源: 题型:
|
| 1 |
| π |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| x-1 | x+a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com