
����Ŀ�������н��ܲ�����2018��4�¶Թ����г���ִ�еġ����ޡ����߽����˵���������������й�A�տ�С����ӵ�к������������һ����ʻ��һ������ͣ�ĵ�Ȩ����Ϊͳ�ƿ�������ʵʩ�������һ���ڳ����Ľ�ͨ����״�����н��ܲ��ų�ȡ��ij��30���ڵ��վ�����������ʵ�����������жԱȣ���ֵ��Ϊ![]() �����ñ�ֵ������1��Ϊ����ͨ���������Ϊ��ӵ�¡�����ͼ��ʾ�ij����ͼʵ�ֵĹ����ǣ� ��
�����ñ�ֵ������1��Ϊ����ͨ���������Ϊ��ӵ�¡�����ͼ��ʾ�ij����ͼʵ�ֵĹ����ǣ� ��
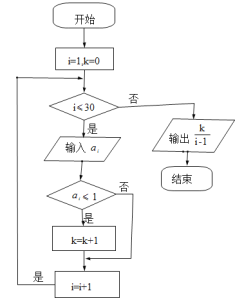
A.��30���ڽ�ͨ�ij�ͨ��B.��30���ڽ�ͨ��ӵ����
C.��30���ڽ�ͨ�ij�ͨ����D.��30���ڽ�ͨ��ӵ������

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() Ϊ����ԭ�㣬
Ϊ����ԭ�㣬![]() ��������
��������![]() ��
��![]() �Ľ��㣬
�Ľ��㣬![]() ��������
��������![]() ��λ�ڵ�һ�����ڵ�����һ�㣬��
��λ�ڵ�һ�����ڵ�����һ�㣬��![]() ��
��![]() ��
��![]() �����Բ��Բ��Ϊ
�����Բ��Բ��Ϊ![]() .
.
��1���Ƿ���ڹ���![]() ��б��Ϊ
��б��Ϊ![]() ��ֱ��
��ֱ��![]() ��ʹ��������
��ʹ��������![]() �ϴ����������ֱ��
�ϴ����������ֱ��![]() �Գƣ������ڣ����
�Գƣ������ڣ����![]() �ķ�Χ���������ڣ�˵�����ɣ�
�ķ�Χ���������ڣ�˵�����ɣ�
��2���Ƿ���ڵ�![]() ��ʹ��ֱ��
��ʹ��ֱ��![]() ��������
��������![]() �����ڵ�
�����ڵ�![]() �������ڣ������
�������ڣ������![]() �����ꣻ�������ڣ�˵������.
�����ꣻ�������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��Բ
��Բ![]() ����R���ֱ��
����R���ֱ��![]() ��Բ��M��N�����R����ֱ��
��Բ��M��N�����R����ֱ��![]() ��SM��Q��.
��SM��Q��.
��1����Q��Ĺ켣���̣�
��2����A��BΪQ�Ĺ켣��x������ҽ��㣬![]() Ϊ�ù켣����һ���㣬��ֱ��AP��BP�ֱ�ֱ��l��
Ϊ�ù켣����һ���㣬��ֱ��AP��BP�ֱ�ֱ��l��![]() �ڵ�M��N���ж���MNΪֱ����Բ�Ƿ�����㡣��Բ�����㣬������ö��㣻�粻�ǣ�˵������.
�ڵ�M��N���ж���MNΪֱ����Բ�Ƿ�����㡣��Բ�����㣬������ö��㣻�粻�ǣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ![]() �У���б��Ϊ
�У���б��Ϊ![]() ��ֱ��
��ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() Ϊ������.��������ԭ��Ϊ���㣬
Ϊ������.��������ԭ��Ϊ���㣬![]() ��������Ϊ����ļ�����ϵ�У�����
��������Ϊ����ļ�����ϵ�У�����![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() .
.
��1����ֱ��![]() ����ͨ����������
����ͨ����������![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
��2����ֱ��![]() ������
������![]() ����
����![]() ��
��![]() ���㣬��
���㣬��![]() ����ֱ��
����ֱ��![]() ����б��.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��ȡ�ü�Сֵ
��ȡ�ü�Сֵ![]() ��
��
��1����ʵ��![]() ��ֵ��
��ֵ��
��2����![]() �����ۺ���
�����ۺ���![]() ����������
����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�������ԭ��Ϊ���㣬
�У�������ԭ��Ϊ���㣬![]() ��������Ϊ���Ὠ��������ϵ������C1�ļ����귽��Ϊ
��������Ϊ���Ὠ��������ϵ������C1�ļ����귽��Ϊ![]() ��C1������һ��P��ֱ������Ϊ
��C1������һ��P��ֱ������Ϊ![]() ��ͨ���任
��ͨ���任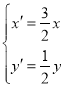 �õ���P�Ķ�Ӧ��
�õ���P�Ķ�Ӧ��![]() ������.
������.
��1�����![]() �Ĺ켣C2��ֱ�����귽�̣�
�Ĺ켣C2��ֱ�����귽�̣�
��2��ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ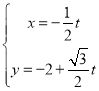 ��
��![]() ��������
Ϊ��������![]() ��C2�ڵ�M��N����
��C2�ڵ�M��N����![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�ƽ��
�У�ƽ��![]() ƽ��
ƽ��![]() ��
��![]() ��
��![]() �ı���
�ı���![]() Ϊƽ���ı���.
Ϊƽ���ı���.
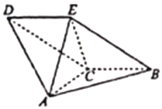
��1��֤����![]() ��
��
��2����![]() ��������
��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�����꼶��1000��ѧ�����������ư�ѧ��ռ80%��ȫ�����ư�ѧ���μ�һ�ο��ԣ����Գɼ����Ƶط�����̬�ֲ�N��72��36���������Գɼ�������60��Ϊ������˴ο��Գɼ����������ԼΪ�� ��
���ο����ݣ���Z��N��������2������P����������Z����+������0.6826��P������2����Z����+2������0.9544��P������3����Z����+3������0.9974��
A.778B.780C.782D.784
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�����![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() ����
Ϊ����![]() ����������ԭ��Ϊ���㣬x��Ǹ�����Ϊ����ļ�����ϵ�У�����
����������ԭ��Ϊ���㣬x��Ǹ�����Ϊ����ļ�����ϵ�У�����![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ��
��
![]() ��
��![]() �
д��![]() ����ͨ���̺�
����ͨ���̺�![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
![]() ��
��![]() ��
��![]() ��
��![]() �ཻ��A��B���㣬��
�ཻ��A��B���㣬��![]() �������
�������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com