
【题目】(本小题满分![]() 分)
分)
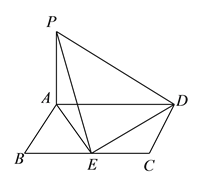
如图,平行四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,点
,点![]() 为
为![]() 中点,连结
中点,连结![]() 、
、![]() .
.
(Ⅰ)若![]() ,
, ![]() ,求证:平面
,求证:平面![]() 平面
平面![]() .
.
(Ⅱ)若![]() ,试探究在直线
,试探究在直线![]() 上有几个点
上有几个点![]() ,使得
,使得![]() ,并说明理由.
,并说明理由.
【答案】详见解析
【解析】试题分析:(1)要证明平面![]() 平面
平面![]() ,即证明
,即证明![]() 平面
平面![]() ,进而转证线线垂直即可;(2)假设
,进而转证线线垂直即可;(2)假设![]() 边上存在
边上存在![]() 使得
使得![]() ,则连结
,则连结![]() ,必有
,必有![]() ,故问题转化为:在
,故问题转化为:在![]() 边上是否存在点
边上是否存在点![]() ,使得
,使得![]() .由平面几何知识,问题又可转化为:以
.由平面几何知识,问题又可转化为:以![]() 为直径的圆与
为直径的圆与![]() 有几个交点.
有几个交点.
试题解析:
(![]() )证明:当
)证明:当![]() ,
, ![]() 时,
时,
∵![]() 是平行四边形,
是平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 中点,
中点,
∴![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() .
.
又∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() 平面
平面![]() .
.
又∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(![]() )假设
)假设![]() 边上存在
边上存在![]() 使得
使得![]() ,则连结
,则连结![]() ,必有
,必有![]() ,故问题转化为:在
,故问题转化为:在![]() 边上是否存在点
边上是否存在点![]() ,使得
,使得![]() .由平面几何知识,问题又可转化为:以
.由平面几何知识,问题又可转化为:以![]() 为直径的圆与
为直径的圆与![]() 有几个交点.
有几个交点.
∵![]() ,
, ![]() ,∴以
,∴以![]() 为直径的圆圆心到直线
为直径的圆圆心到直线![]() 的距离
的距离![]() ,半径为
,半径为![]() .
.
易知当![]() 时,以
时,以![]() 为直径的圆与
为直径的圆与![]() 无交点,
无交点,
当![]() 时,以
时,以![]() 为直径的圆与
为直径的圆与![]() 有且只有一个交点,
有且只有一个交点,
当![]() 时,以
时,以![]() 为直径的圆与
为直径的圆与![]() 有
有![]() 个交点.
个交点.
故当![]() 时,直线
时,直线![]() 上不存在点
上不存在点![]() ,使得
,使得![]() .
.
当![]() 时,直线
时,直线![]() 上存在一个点
上存在一个点![]() ,使得
,使得![]() .
.
当![]() 时,直线
时,直线![]() 上存在
上存在![]() 个点
个点![]() ,使得
,使得![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cosx(x∈(0,2π))有两个不同的零点x1、x2 , 方程f(x)=m有两个不同的实根x3、x4 . 若把这四个数按从小到大排列构成等差数列,则实数m的值为( )
A.![]()
B.![]()
C.![]()
D.- ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当今,手机已经成为人们不可或缺的交流工具,人们常常把喜欢玩手机的人冠上了名号“低头族”,手机已经严重影响了人们的生活.—媒体为调查市民对低头族的认识,从某社区的500名市民中随机抽取![]() 名市民,按年龄情况进行统计的频率分布表和频率分布直方图如图:
名市民,按年龄情况进行统计的频率分布表和频率分布直方图如图:


(1)求出表中![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)媒体记者为了做好调查工作,决定在第2,4,5组中用分层抽样的方法抽取6名市民进行问卷调查, 再从这6名市民中随机抽取2名接受电视采访,求第2组至少有一名接受电视采访的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海域的东西方向上分别有A,B两个观测点(如图),它们相距![]() 海里.现有一艘轮船在D点发出求救信号,经探测得知D点位于A点北偏东45°,B点北偏西60°,这时,位于B点南偏西60°且与B点相距
海里.现有一艘轮船在D点发出求救信号,经探测得知D点位于A点北偏东45°,B点北偏西60°,这时,位于B点南偏西60°且与B点相距![]() 海里的C点有一救援船,其航行速度为30海里/小时.
海里的C点有一救援船,其航行速度为30海里/小时.

(1)求B点到D点的距离BD;
(2)若命令C处的救援船立即前往D点营救,求该救援船到达D点需要的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}中公差d≠0,有a1+a4=14,且a1,a2,a7成等比数列.
(Ⅰ)求{an}的通项公式an与前n项和公式Sn;
(Ⅱ)令bn=![]() (k<0),若{bn}是等差数列,求数列{
(k<0),若{bn}是等差数列,求数列{![]() }的前n项和Tn.
}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度![]() (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度![]() (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当![]() 不超过
不超过![]() 尾/立方米时,
尾/立方米时, ![]() 的值为
的值为![]() 千克/年;当
千克/年;当![]() 时,
时, ![]() 是
是![]() 的一次函数,且当
的一次函数,且当![]() 时,
时, ![]() .
.
(![]() )当
)当![]() 时,求
时,求![]() 关于
关于![]() 的函数的表达式.
的函数的表达式.
(![]() )当养殖密度
)当养殖密度![]() 为多大时,每立方米的鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
为多大时,每立方米的鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知坐标平面上点![]() 与两个定点
与两个定点![]() ,
, ![]() 的距离之比等于5.
的距离之比等于5.
(1)求点![]() 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形;
(2)记(1)中的轨迹为![]() ,过点
,过点![]() 的直线
的直线![]() 被
被![]() 所截得的线段的长为8,求直线
所截得的线段的长为8,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com