
已知圆C: 与直线l:
与直线l: ,且直线l被圆C截得的弦长为
,且直线l被圆C截得的弦长为 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)当 时,求过点(3,5)且与圆C相切的直线方程.
时,求过点(3,5)且与圆C相切的直线方程.
(Ⅰ) 或
或 ;(Ⅱ)
;(Ⅱ)
解析试题分析:该题考察学生直线和圆的位置关系、点到直线的距离等基础知识,考察学生数形结合、逻辑思维,基本的运算能力,(Ⅰ)直线被圆所截得的弦长的计算一般放在直角三角形中利用勾股定理处理(圆心、弦的端点、弦的中点为顶点),先求圆心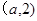 到直线l:
到直线l: 的直线,然后根据勾股定理列方程可得
的直线,然后根据勾股定理列方程可得 或
或 ;(Ⅱ)当
;(Ⅱ)当 时,∴
时,∴ ,先设切线方程为:
,先设切线方程为: ,进而化为一般式方程
,进而化为一般式方程 ,利用圆心到直线的距离等于半径列方程,可求得
,利用圆心到直线的距离等于半径列方程,可求得
试题解析:(Ⅰ)由已知可得圆C的圆心为 ,半径为2,则圆心到直线的距离为
,半径为2,则圆心到直线的距离为 ,
,
由勾股定理 ,解得
,解得 或
或
(Ⅱ)当 时,圆的方程为
时,圆的方程为 。设切线的方程为
。设切线的方程为 ,由
,由 ,解得
,解得 ,
,
所以所求切线方程为 .
.
考点:1、直线和圆的位置关系;2、点到直线的距离公式.


科目:高中数学 来源: 题型:解答题
已知圆 的圆心在直线
的圆心在直线 上,且与
上,且与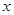 轴交于两点
轴交于两点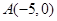 ,
,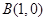 .
.
(1)求圆 的方程;
的方程;
(2)求过点
 的圆
的圆 的切线方程;
的切线方程;
(3)已知 ,点
,点 在圆
在圆 上运动,求以
上运动,求以 ,
, 为一组邻边的平行四边形的另一个顶点
为一组邻边的平行四边形的另一个顶点 轨迹方程.
轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在平面直角坐标系 中,点
中,点 ,直线
,直线 。设圆
。设圆 的半径为
的半径为 ,圆心在
,圆心在 上。
上。
(1)若圆心 也在直线
也在直线 上,过点
上,过点 作圆
作圆 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆 上存在点
上存在点 ,使
,使 ,求圆心
,求圆心 的横坐标
的横坐标 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知 是抛物线
是抛物线 上的点,
上的点, 是
是 的焦点, 以
的焦点, 以 为直径的圆
为直径的圆 与
与 轴的另一个交点为
轴的另一个交点为 .
.
(Ⅰ)求 与
与 的方程;
的方程;
(Ⅱ)过点 且斜率大于零的直线
且斜率大于零的直线 与抛物线
与抛物线 交于
交于 两点,
两点, 为坐标原点,
为坐标原点, 的面积为
的面积为 ,证明:直线
,证明:直线 与圆
与圆 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在平面直角坐标系 中,点
中,点 ,直线
,直线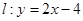 ,设圆
,设圆 的半径为1, 圆心在
的半径为1, 圆心在 上.
上.
(1)若圆心 也在直线
也在直线 上,过点
上,过点 作圆
作圆 的切线,求切线方程;
的切线,求切线方程;
(2)若圆 上存在点
上存在点 ,使
,使 ,求圆心
,求圆心 的横坐标
的横坐标 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
己知圆 直线
直线 .
.
(1) 求与圆 相切, 且与直线
相切, 且与直线 平行的直线
平行的直线 的方程;
的方程;
(2) 若直线 与圆
与圆 有公共点,且与直线
有公共点,且与直线 垂直,求直线
垂直,求直线 在
在 轴上的截距
轴上的截距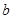 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com