
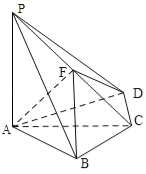
【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=![]() ,F为PC的中点,AF⊥PB.
,F为PC的中点,AF⊥PB.
(1)求PA的长;
(2)求二面角B﹣AF﹣D的正弦值.
【答案】(1)2![]() (2)
(2)![]()
【解析】(1)如图,连接BD交AC于点O
∵BC=CD,AC平分角BCD,∴AC⊥BD
以O为坐标原点,OB、OC所在直线分别为x轴、y轴,
建立空间直角坐标系O﹣xyz,
则OC=CDcos![]() =1,而AC=4,可得AO=AC﹣OC=3.
=1,而AC=4,可得AO=AC﹣OC=3.
又∵OD=CDsin![]() =
=![]() ,
,
∴可得A(0,﹣3,0),B(![]() ,0,0),C(0,1,0),D(﹣
,0,0),C(0,1,0),D(﹣![]() ,0,0)
,0,0)
由于PA⊥底面ABCD,可设P(0,﹣3,z)
∵F为PC边的中点,∴F(0,﹣1,![]() ),由此可得
),由此可得![]() =(0,2,
=(0,2,![]() ),
),
∵![]() =(
=(![]() ,3,﹣z),且AF⊥PB,
,3,﹣z),且AF⊥PB,
∴![]()
![]() =6﹣
=6﹣![]() =0,解之得z=2
=0,解之得z=2![]() (舍负)
(舍负)
因此,![]() =(0,0,﹣2
=(0,0,﹣2![]() ),可得PA的长为2
),可得PA的长为2![]() ;
;
(2)由(1)知![]() =(﹣
=(﹣![]() ,3,0),
,3,0),![]() =(
=(![]() ,3,0),
,3,0),![]() =(0,2,
=(0,2,![]() ),
),
设平面FAD的法向量为![]() =(x1,y1,z1),平面FAB的法向量为
=(x1,y1,z1),平面FAB的法向量为![]() =(x2,y2,z2),
=(x2,y2,z2),
∵![]()
![]() =0且
=0且![]()
![]() =0,∴
=0,∴ ,取y1=
,取y1=![]() 得
得![]() =(3,
=(3,![]() ,﹣2),
,﹣2),
同理,由![]()
![]() =0且
=0且![]()
![]() =0,解出
=0,解出![]() =(3,﹣
=(3,﹣![]() ,2),
,2),
∴向量![]() 、
、![]() 的夹角余弦值为cos<
的夹角余弦值为cos<![]() ,
,![]() >=
>=![]() =
=![]() =
=![]()
因此,二面角B﹣AF﹣D的正弦值等于![]() =
=![]()



科目:高中数学 来源: 题型:
【题目】某保险公司决定每月给推销员确定个具体的销售目标,对推销员实行目标管理.销售目标确定的适当与否,直接影响公司的经济效益和推销员的工作积极性,为此,该公司当月随机抽取了50位推销员上个月的月销售额(单位:万元),绘制成如图所示的频率分布直方图.

(1)①根据图中数据,求出月销售额在![]() 小组内的频率.
小组内的频率.
②根据直方图估计,月销售目标定为多少万元时,能够使70%的推销员完成任务?并说明理由.
(2)该公司决定从月销售额为![]() 和
和![]() 的两个小组中,选取2位推销员介绍销售经验,求选出的推销员来自同一个小组的概率.
的两个小组中,选取2位推销员介绍销售经验,求选出的推销员来自同一个小组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() 为参数),A,B是C上的动点,且满足
为参数),A,B是C上的动点,且满足![]() (O为坐标原点),以原点O为极点,x轴的正半轴为极轴建立坐标系,点D的极坐标为
(O为坐标原点),以原点O为极点,x轴的正半轴为极轴建立坐标系,点D的极坐标为![]() .
.
(1)求椭圆C的极坐标方程和点D的直角坐标;
(2)利用椭圆C的极坐标方程证明 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区工会利用“健步行![]() ”开展明年健步走积分奖励活动.会员每天走5千步可获积分30分(不足5千步不积分),每多走2千步再积20分(不足2千步不积分).为了解会员的健步走情况,工会在某天从系统中随机抽取了1000名会员,统计了当天他们的步数,并将样本数据分为
”开展明年健步走积分奖励活动.会员每天走5千步可获积分30分(不足5千步不积分),每多走2千步再积20分(不足2千步不积分).为了解会员的健步走情况,工会在某天从系统中随机抽取了1000名会员,统计了当天他们的步数,并将样本数据分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 九组,整理得到如下频率分布直方图:
九组,整理得到如下频率分布直方图:
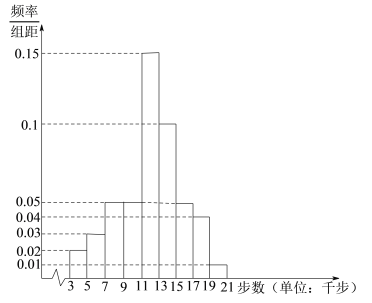
(1)从当天步数在![]() ,
,![]() ,
,![]() 的会员中按分层抽样的方式抽取6人,再从这6人中随机抽取2人,求这2人积分之和不少于220分的概率;
的会员中按分层抽样的方式抽取6人,再从这6人中随机抽取2人,求这2人积分之和不少于220分的概率;
(2)求该组数据的中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C经过点![]() ,
,![]() ,且圆心在直线
,且圆心在直线![]() 上
上
(1)求圆C的方程.
(2)过点![]() 的直线与圆C交于A,B两点,问:在直线
的直线与圆C交于A,B两点,问:在直线![]() 上是否存在定点N,使得
上是否存在定点N,使得![]() (
(![]() ,
,![]() 分别为直线AN,BN的斜率)恒成立?若存在,请求出点N的坐标;若不存在,请说明理由.
分别为直线AN,BN的斜率)恒成立?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表所示(单位辆),若按A,B,C三类用分层抽样的方法在这个月生产的轿车中抽取50辆,则A类轿车有10辆
轿车A | 轿车B | 轿车C | |
舒适型 | 100 | 150 | z |
标准型 | 300 | 450 | 600 |
(1)求下表中z的值;
(2)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:94,86,92,96,87,93,90,82把这8辆轿车的得分看作一个总体,从中任取一个得分数![]() 记这8辆轿车的得分的平均数为
记这8辆轿车的得分的平均数为![]() ,定义事件
,定义事件![]() {
{![]() ,且函数
,且函数![]() 没有零点},求事件
没有零点},求事件![]() 发生的概率
发生的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
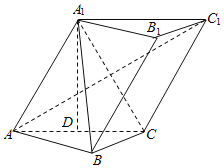
【题目】如图,三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=AA1=A1C=2,平面ACC1A1⊥平面ABC.现以边AC的中点D为坐标原点,平面ABC内垂直于AC的直线为![]() 轴,直线AC为
轴,直线AC为![]() 轴,直线DA1为
轴,直线DA1为![]() 轴建立空间直角坐标系,解决以下问题:
轴建立空间直角坐标系,解决以下问题:
(1)求异面直线AB与A1C所成角的余弦值;
(2)求直线AB与平面A1BC所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com