
【题目】我们把定义在![]() 上,且满足
上,且满足![]() (其中常数
(其中常数![]() ,
,![]() 满足
满足![]() ,
,![]() ,
,![]() )的函数叫做似周期函数.
)的函数叫做似周期函数.
(1)若某个似周期函数![]() 满足
满足![]() 且图像关于直线
且图像关于直线![]() 对称,求证:函数
对称,求证:函数![]() 是偶函数;
是偶函数;
(2)当![]() ,
,![]() 时,某个似周期函数在
时,某个似周期函数在![]() 时的解析式为
时的解析式为![]() ,求函数
,求函数![]() ,
,![]() 的解析式;
的解析式;
(3)对于确定的![]() 且当
且当![]() 时,
时,![]() ,试研究似周期函数
,试研究似周期函数![]() 在区间
在区间![]() 上是否可能是单调函数?若可能,求出
上是否可能是单调函数?若可能,求出![]() 的取值范围;若不可能,请说明理由.
的取值范围;若不可能,请说明理由.
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() 的参数方程为
的参数方程为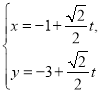 (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]()
![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点.
两点.
(1)求曲线![]() 与直线
与直线![]() 交点的极坐标(
交点的极坐标(![]() ,
,![]() );
);
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,AC⊥BC,且,AC=BC=2,D,E分别为AB,PB中点,PD⊥平面ABC,PD=3.
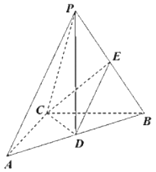
(1)求直线CE与直线PA夹角的余弦值;
(2)求直线PC与平面DEC夹角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近一段时间来,由于受非洲猪瘟的影响,各地猪肉价格普遍上涨,生猪供不应求。各大养猪场正面临巨大挑战,目前各项针对性政策措施对于生猪整体产能恢复、激发养殖户积极性的作用正在逐步显现.
现有甲、乙两个规模一致的大型养猪场,均养有1万头猪.根据猪的重量,将其分为三个成长阶段如下表.
猪生长的三个阶段
阶段 | 幼年期 | 成长期 | 成年期 |
重量(Kg) |
|
|
|
根据以往经验,两个养猪场内猪的体重![]() 均近似服从正态分布
均近似服从正态分布![]()
![]() .
.
由于我国有关部门加强对大型养猪场即将投放市场的成年期的猪监控力度,高度重视其质量保证,为了养出健康的成年活猪,甲、乙两养猪场引入两种不同的防控及养殖模式.已知甲、乙两个养猪场内一头成年期猪能通过质检合格的概率分别为![]() ,
,![]() .
.
(1)试估算各养猪场三个阶段的猪的数量;
(2)已知甲养猪场出售一头成年期的猪,若为健康合格的猪 ,则可盈利![]() 元,若为不合格的猪,则亏损
元,若为不合格的猪,则亏损![]() 元;乙养猪场出售一头成年期的猪,若为健康合格的猪 ,则可盈利
元;乙养猪场出售一头成年期的猪,若为健康合格的猪 ,则可盈利![]() 元,若为不合格的猪,则亏损
元,若为不合格的猪,则亏损![]() 元.记
元.记![]() 为甲、乙养猪场各出售一头成年期猪所得的总利润,求随机变量
为甲、乙养猪场各出售一头成年期猪所得的总利润,求随机变量![]() 的分布列,假设两养猪场均能把成年期猪售完,求两养猪场的总利润期望值.
的分布列,假设两养猪场均能把成年期猪售完,求两养猪场的总利润期望值.
(参考数据:若![]() ,则
,则![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“更相减损术”是《九章算术》中介绍的一种用于求两个正整数的最大公约数的方法,该方法的算法流程如图所示,根据程序框图计算,当a=35,b=28时,该程序框图运行的结果是( )
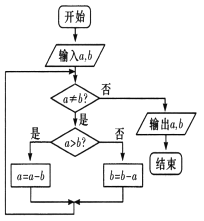
A.a=6,b=7B.a=7,b=7C.a=7,b=6D.a=8,b=8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面ABCD为梯形,AB//CD,
中,底面ABCD为梯形,AB//CD,![]() ,AB=AD=2CD=2,△ADP为等边三角形.
,AB=AD=2CD=2,△ADP为等边三角形.

(1)当PB长为多少时,平面![]() 平面ABCD?并说明理由;
平面ABCD?并说明理由;
(2)若二面角![]() 大小为150°,求直线AB与平面PBC所成角的正弦值.
大小为150°,求直线AB与平面PBC所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com