
【题目】已知数列{an}中,a1=1,an+1=![]() ,(n∈N*)
,(n∈N*)
(1)求数列{an}的通项公式an,
(2)若数列{bn}满足bn=(3n﹣1)![]() an,数列{bn}的前n项和为Tn,若不等式(﹣1)nλ<Tn对一切n∈N*恒成立,求λ的取值范围.
an,数列{bn}的前n项和为Tn,若不等式(﹣1)nλ<Tn对一切n∈N*恒成立,求λ的取值范围.
【答案】(1)an=![]() .(2)﹣1<λ<2.
.(2)﹣1<λ<2.
【解析】
试题(1)由已知条件推导出![]() ,从而得到
,从而得到![]() =(
=(![]() )3n﹣1=
)3n﹣1=![]() .由此能求出结果.
.由此能求出结果.
(2)由![]() =
=![]() ,利用裂项求和法求出
,利用裂项求和法求出![]() ,从而得到{Tn}为单调递增数列,由此利用分类讨论思想能求出λ的取值范围.
,从而得到{Tn}为单调递增数列,由此利用分类讨论思想能求出λ的取值范围.
解:(1)∵数列{an}中,a1=1,an+1=![]() ,(n∈N*)
,(n∈N*)
∴![]() =
=![]() ,
,
∴![]() ,
,
∴![]() =(
=(![]() )3n﹣1=
)3n﹣1=![]() .
.
∴an=![]() .
.
(2)∵![]() ,bn=(3n﹣1)
,bn=(3n﹣1)![]() an,
an,
∴![]() =
=![]() ,
,
∴![]() ,①
,①
![]() ,②
,②
①﹣②,得![]()
=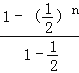 ﹣
﹣![]()
=2﹣![]() ,
,
∴![]() .,
.,
∵Tn+1﹣Tn=(4﹣![]() )﹣(4﹣
)﹣(4﹣![]() )=
)=![]() ,
,
∴{Tn}为单调递增数列,
∵不等式(﹣1)nλ<Tn对一切n∈N*恒成立,
∴①当n为正奇数时,﹣λ<Tn对一切正奇数成立,
∴(Tn)min=T1=1,∴﹣λ<1,∴λ>﹣1;
②当n为正偶数时,λ<Tn对一切正偶数成立,
∵(Tn)min=T2=2,∴λ<2.
综上知﹣1<λ<2.


科目:高中数学 来源: 题型:
【题目】已知椭圆C的两个顶点分别为A(2,0),B(2,0),焦点在x轴上,离心率为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)点D为x轴上一点,过D作x轴的垂线交椭圆C于不同的两点M,N,过D作AM的垂线交BN于点E.求证:△BDE与△BDN的面积之比为4:5.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面是菱形,
的底面是菱形,![]() 底面
底面![]() ,
,![]() 分别是
分别是![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() .
.
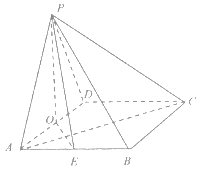
(I)证明:![]() ;
;
(II)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(III)在![]() 边上是否存在点
边上是否存在点![]() ,使
,使![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() ,若存在,确定点
,若存在,确定点![]() 位置;若不存在,说明理由.
位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(选做题)
A.[选修4-2:矩阵与变换](本小题满分10分)
已知m,n∈R,向量![]() 是矩阵
是矩阵![]() 的属于特征值3的一个特征向量,求矩阵M及另一个特征值.
的属于特征值3的一个特征向量,求矩阵M及另一个特征值.
B.[选修4-4:坐标系与参数方程](本小题满分10分)
在平面直角坐标系xOy中,已知直线![]() 的参数方程为
的参数方程为![]() ( t为参数),椭圆C的参数方程为
( t为参数),椭圆C的参数方程为![]() .设直线
.设直线![]() 与椭圆C交于A,B两点,求线段AB的长.
与椭圆C交于A,B两点,求线段AB的长.
C.[选修4-5:不等式选讲](本小题满分10分)
已知x,y,z均是正实数,且![]() 求证:
求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆形纸片的圆心为O,半径为5,该纸片上的等边三角形ABC的中心为O,点D,E,F为圆O上的点,![]() ,
,![]() ,
,![]() 分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起
分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起![]() ,
,![]() ,
,![]() ,使得D,E,F重合于P,得到三棱锥
,使得D,E,F重合于P,得到三棱锥![]() .
.

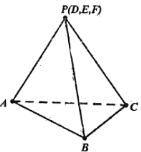
(1)当![]() 时,求三棱锥
时,求三棱锥![]() 的体积;
的体积;
(2)当![]() 的边长变化时,三棱锥
的边长变化时,三棱锥![]() 的侧面和底面所成二面角为
的侧面和底面所成二面角为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱锥D-ABC中,二面角A-BC-D的大小为90°,且∠BDC=90°,∠ABC=30°,BC=3,![]() .
.
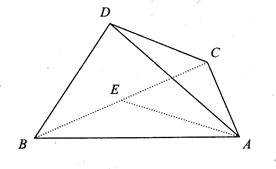
(1)求证:AC⊥平面BCD;
(2)二面角B-AC-D为45°,且E为线段BC的中点,求直线AE与平面ACD所成的角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com