解:(Ⅰ)∵

=(Asinωx,Acosωx),

=(cosθ,sinθ),
∴f(x)=
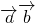
+1=Asinωxcosθ+Acosωxsinθ+1
=Asin(ωx+θ)+1,
因为f(x)的图象的两个相邻对称中心的距离为
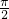
,且当
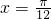
时,f(x)取得最大值3.
所以A=2,

,解得ω=2,故f(x)=2sin(2x+θ)+1,
由f(
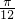
)=2sin(2×
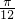
+θ)+1=3,解得

.
故f(x)的解析式为:f(x)=2sin(2x+

)+1
(Ⅱ)由(Ⅰ)可知:将f(x)的图象先向下平移1个单位得函数y=2sin(2x+

)的图象,
再向左平移?(?>0)个单位得g(x)的图象,则g(x)=2sin[2(x+?)+

],若g(x)为奇函数,
则g(0)=2sin(2?+

),即2?+

=kπ,(k∈Z),又?>0,故?的最小值为

分析:(Ⅰ)由已知可得f(x)=Asin(ωx+θ)+1,再由f(x)的图象的两个相邻对称中心的距离为
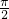
,且当
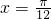
时,f(x)取得最大值3,可解A,w,θ;
(II)先由图象变换的规律解得g(x)的解析式,再由奇函数的性质得g(0)=0可求?的最小值.
点评:本题为向量与三角函数的综合应用,涉及数量积和图象的变换以及奇函数的特点,属中档题.

 =(Asinωx,Acosωx),
=(Asinωx,Acosωx), =(cosθ,sinθ),f(x)=
=(cosθ,sinθ),f(x)= •
• +1,其中A>0、ω>0、θ为锐角.f(x)的图象的两个相邻对称中心的距离为
+1,其中A>0、ω>0、θ为锐角.f(x)的图象的两个相邻对称中心的距离为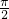 ,且当
,且当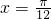 时,f(x)取得最大值3.
时,f(x)取得最大值3. =(Asinωx,Acosωx),
=(Asinωx,Acosωx), =(cosθ,sinθ),
=(cosθ,sinθ),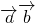 +1=Asinωxcosθ+Acosωxsinθ+1
+1=Asinωxcosθ+Acosωxsinθ+1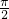 ,且当
,且当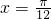 时,f(x)取得最大值3.
时,f(x)取得最大值3. ,解得ω=2,故f(x)=2sin(2x+θ)+1,
,解得ω=2,故f(x)=2sin(2x+θ)+1,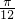 )=2sin(2×
)=2sin(2×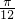 +θ)+1=3,解得
+θ)+1=3,解得 .
. )+1
)+1 )的图象,
)的图象, ],若g(x)为奇函数,
],若g(x)为奇函数, ),即2?+
),即2?+ =kπ,(k∈Z),又?>0,故?的最小值为
=kπ,(k∈Z),又?>0,故?的最小值为
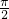 ,且当
,且当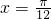 时,f(x)取得最大值3,可解A,w,θ;
时,f(x)取得最大值3,可解A,w,θ;

 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案 ,函数
,函数 .
.