B
分析:由f(x)是偶函数说明函数图象关于y轴对称,再由f(x-1)是奇函数说明函数图象关于点(-1,0)对称,因此可以证明出函数的周期为4.只要找出方程f(x)+4=f(1)在在区间(-2,2)内实根的情况,就不难找到f(x)+4=f(1)在区间(-2,10)内的所有实根之和了.
解答:根据题意,f(1)=log
31=0,
因此方程f(x)+4=f(1)化简为f(x)=-4
当0<x≤1时,f(x)=log
3x=-4,可得

因为f(x)是偶函数,所以当-1≤x<0时,f(x)=log
3-(-x)=-4,
可得

,
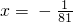
∵f(x-1)是奇函数,图象关于点(-1,0)对称
∴当-2<x≤-1时的函值域与当-1≤x<0时函数值域互为相反数,f(x)≥0,方程f(x)=-4没有实根
再根据f(x)是偶函数,图象关于点y轴对称得,当-2<x≤-1时的函值域与当1≤x<2时函数值域相同,
f(x)≥0,方程f(x)=-4没有实根
因此函数在(-2,2)只有两个实数根

又∵f(2-x)=f(x-2)=f(-1+(x-1))=-f(-1-(x-1))=-f(-x)
∴f(2+x)=-f(x)?f(4+x)=-f(2+x)=f(x)
函数的周期为4
因此可得在(2,6)只有两个实数根
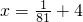
,在(6,10)只有两个实数根
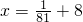
因此可得六个实数根的和为

=24
故选B
点评:本题考查了函数与方程的综合应用以及函数图象的对称性与奇偶性等知识点,属于难题.充分利用函数的奇偶性与周期性,熟练对数的运算性质是解决本题的关键.


 ,
,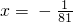

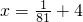 ,在(6,10)只有两个实数根
,在(6,10)只有两个实数根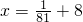
 =24
=24

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案