
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 本题利用画图结合运动变化的思想进行分析.我们不妨先将 A、B、C 按如图所示放置,容易看出此时 BC<AB=AC.
现在,我们将 A 和 B 往上移,并且总保持 AB=AC(这是可以做到的,只要 A、B 的速度满足一定关系),而当A、B 移得很高很高时,就得到①和②都是正确的.至于③,结合条件利用反证法的思想方法进行说明即可
解答 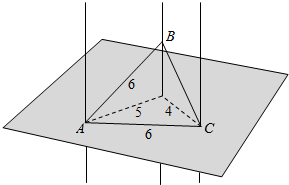 解:我们不妨先将 A、B、C按如图所示放置.
解:我们不妨先将 A、B、C按如图所示放置.
容易看出此时 BC<AB=AC.
现在,我们将 A 和 B 往上移,
并且总保持AB=AC(这是可以做到的,
只要 A、B 的速度满足一定关系),
而当A、B 移得很高很高时,
不难想象△ABC 将会变得很扁,
也就是会变成顶角A“非常钝”的一个等腰钝角三角形.
于是,在移动过程中,
总有一刻,使△ABC 成为等边三角形,
亦总有另一刻,使△ABC成为直角三角形(而且还是等腰的).
这样,就得到①和②都是正确的.
至于③,如图所示.
为方便书写,称三条两两垂直的棱所共的顶点为?.
假设A是?,
那么由 AD⊥AB,AD⊥AC,
知 L3⊥△ABC,
从而△ABC 三边的长就是三条直线的距离4、5、6,
这就与AB⊥AC 矛盾.
同理可知D是?时也矛盾;
假设C是?,
那么由BC⊥CA,BC⊥CD,
知BC⊥△CAD,
而 l1∥△CAD,故 BC⊥l1,
从而 BC 为 l1与 l2 的距离,
于是 EF∥BC,EF=BC,这样就得到 EF⊥FG,矛盾.
同理可知 B 是?时也矛盾.
综上,不存在四点Ai(i=1,2,3,4),
使得四面体A1A2A3A4为在一个顶点处的三条棱两两互相垂直的四面体.
故选:C.
点评 本题考查命题真假的判断解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
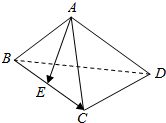
| A. | $\overrightarrow{AE}•\overrightarrow{BC}$<$\overrightarrow{AE}•\overrightarrow{CD}$ | B. | $\overrightarrow{AE}•\overrightarrow{BC}$=$\overrightarrow{AE}•\overrightarrow{CD}$ | ||
| C. | $\overrightarrow{AE}•\overrightarrow{BC}$>$\overrightarrow{AE}•\overrightarrow{CD}$ | D. | $\overrightarrow{AE}•\overrightarrow{BC}$与$\overrightarrow{AE}•\overrightarrow{CD}$大小不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com