
分析 (1)可以判断a=0时,f(x)为偶函数,从而图象关于y轴对称,并且可求出f(1)=0,从而说明p,q都是真命题,这样即可判断¬p,p∨q,p∧q的真假;
(2)先根据f(x)的值域为R,便有△=a2-4a≥0,这样可得到a≤0,或a≥4,并且可以看出,要使得f(x)和g(x)的图象恰有两个交点,则需x2-(a+1)x+a=0有两个不同的正根,从而a要满足$\left\{\begin{array}{l}{△>0}\\{a+1>0}\\{a>0}\end{array}\right.$,解该不等式组即可得出实数a的取值范围;
(3)首先要使函数f(x)和f($\frac{1}{x}$)有意义,从而有x2-ax+a>0和$\frac{1}{{x}^{2}}-\frac{a}{x}+a>0$都恒成立,这样即可得出$4≤a<\frac{9}{2}$,然后求导数:$f′(x)和f′(\frac{1}{x})$,容易说明$f′(x)>0,f′(\frac{1}{x})>0$,从而说明4$≤a<\frac{9}{2}$时,满足函数H(x)在[3,+∞)上单调递增,这样便可得出实数a的取值范围.
解答 解:(1)当a=0时,f(x)=lgx2,显然为偶函数,∴图象关于y轴对称;
∴命题p为真命题;
f(1)=lg1=0,∴f(x)的图象过定点(1,0);
∴命题q为真命题;
∴¬p为假,p∨q为真,p∧q为真;
(2)f(x)的值域为R;
∴△=a2-4a≥0;
∴a≤0,或a≥4;
f(x)与g(x)的图象恰有两个交点;
∴方程x2-ax+a=x恰有两个不同的正根;
即方程x2-(a+1)x+a=0恰有两个不同的正根;
∴$\left\{\begin{array}{l}{△=(a+1)^{2}-4a>0}\\{a+1>0}\\{a>0}\end{array}\right.$;
解得a>0,且a≠1;
∴a≥4;
∴实数a的取值范围为[4,+∞);
(3)根据题意,x2-ax+a>0 ①和$\frac{1}{{x}^{2}}-\frac{a}{x}+a>0$ ②在[3,+∞)上恒成立;
∴由①得,$a<\frac{{x}^{2}}{x-1}$,设h(x)=$\frac{{x}^{2}}{x-1}$,$h′(x)=\frac{{x}^{2}-2x}{(x-1)^{2}}$=$\frac{(x-1)^{2}-1}{(x-1)^{2}}>0$;
∴h(x)在[3,+∞)上单调递增;
∴$h(x)≥h(3)=\frac{9}{2}$;
∴$a<\frac{9}{2}$;
同样,由②得,a≥0;
由前面知,a≤0,或a≥4;
∴$4≤a<\frac{9}{2}$;
$f′(x)=\frac{2x-a}{({x}^{2}-ax+a)ln10}$,$f′(\frac{1}{x})=\frac{1}{{x}^{3}}(ax-2)$;
根据x≥3,$4≤a<\frac{9}{2}$;
∴f′(x)>0,$f′(\frac{1}{x})>0$;
∴H′(x)>0;
即满足H(x)在[3,+∞)上递增;
∴实数a的取值范围为$[4,\frac{9}{2})$.
点评 考查真假命题的概念,偶函数的定义,1的对数等于0,对数函数的值域为R时,定义域的情况如何,一元二次方程实根的情况和判别式△的关系,以及韦达定理,根据导数符号判断函数的单调性,根据函数的单调性求函数的值域.


 全能练考卷系列答案
全能练考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
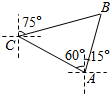 如图所示,一艘海轮从A处出发,测得灯塔在海轮的北偏东15°方向,与海轮相距20海里的B处,海轮按北偏西60°的方向航行了30分钟后到达C处,又测得灯塔在海轮的北偏东75°的方向,则海轮的速度为$\frac{2}{3}$($\sqrt{3}$-1)海里/分钟.
如图所示,一艘海轮从A处出发,测得灯塔在海轮的北偏东15°方向,与海轮相距20海里的B处,海轮按北偏西60°的方向航行了30分钟后到达C处,又测得灯塔在海轮的北偏东75°的方向,则海轮的速度为$\frac{2}{3}$($\sqrt{3}$-1)海里/分钟.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 320 | B. | 384 | C. | 408 | D. | 480 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com