
【题目】已知方程![]() =k在(0,+∞)上有两个不同的解α,β(α<β),则下列的四个命题正确的是( )
=k在(0,+∞)上有两个不同的解α,β(α<β),则下列的四个命题正确的是( )
A. sin 2α=2αcos2α B. cos 2α=2αsin2α
C. sin 2β=-2βsin2β D. cos 2β=-2βsin2β
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=exsinx,其中x∈R,e=2.71828…为自然对数的底数. (Ⅰ)求函数f(x)的单调区间;
(Ⅱ)当 ![]() 时,f(x)≥kx,求实数k的取值范围.
时,f(x)≥kx,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=ax3+bx2+cx的极小值为﹣8,其导函数y=f′(x)的图象经过点 ![]() ,如图所示,
,如图所示, 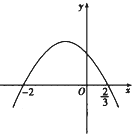
(1)求f(x)的解析式;
(2)若对x∈[﹣3,3]都有f(x)≥m2﹣14m恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=x3+ax2+bx+1的导函数f′(x)满足f′(x)=2a,f′(2)=﹣b,
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)设g(x)=f′(x)ex , 求函数g(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】综合题。
(1)3人坐在有八个座位的一排上,若每人的左右两边都要有空位,则不同坐法的种数为多少?
(2)有5个人并排站成一排,如果甲必须在乙的右边,则不同的排法有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂产生的废气经过过滤后排放,排放时污染物的含量不得超过1%.已知在过滤过程中废气中的污染物数量P(单位:毫克/升)与过滤时间t(单位:小时)之间的函数关系为:P=P0e﹣kt , (k,P0均为正的常数).若在前5个小时的过滤过程中污染物被排除了90%.那么,至少还需( )时间过滤才可以排放.
A.![]() 小时
小时
B.![]() 小时
小时
C.5小时
D.10小时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com